
科目: 来源: 题型:
【题目】定义区间![]() 、
、![]() 、
、![]() 、
、![]() 的长度均为
的长度均为![]() ,已知不等式
,已知不等式![]() 的解集为
的解集为![]() .
.
(1)求![]() 的长度;
的长度;
(2)函数![]() (
(![]() ,
,![]() )的定义域与值域都是
)的定义域与值域都是![]() (
(![]() ),求区间
),求区间![]() 的最大长度;
的最大长度;
(3)关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,若
,若![]() 的长度为6,求实数
的长度为6,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
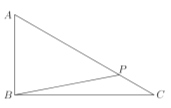
【题目】如图,某公园有三个警卫室![]() 、
、![]() 、
、![]() 有直道相连,
有直道相连,![]() 千米,
千米,![]() 千米,
千米,![]() 千米.
千米.
(1)保安甲沿![]() 从警卫室
从警卫室![]() 出发行至点
出发行至点![]() 处,此时
处,此时![]() ,求
,求![]() 的直线距离;
的直线距离;
(2)保安甲沿![]() 从警卫室
从警卫室![]() 出发前往警卫室
出发前往警卫室![]() ,同时保安乙沿
,同时保安乙沿![]() 从警卫室
从警卫室![]() 出发前往警卫室
出发前往警卫室![]() ,甲的速度为1千米/小时,乙的速度为2千米/小时,若甲乙两人通过对讲机联系,对讲机在公园内的最大通话距离不超过3千米,试问有多长时间两人不能通话?(精确到0.01小时)
,甲的速度为1千米/小时,乙的速度为2千米/小时,若甲乙两人通过对讲机联系,对讲机在公园内的最大通话距离不超过3千米,试问有多长时间两人不能通话?(精确到0.01小时)
查看答案和解析>>
科目: 来源: 题型:
【题目】每年10月中上旬是小麦的最佳种植时间,但小麦的发芽会受到土壤、气候等多方面因素的影响.某科技小组为了解昼夜温差的大小与小麦发芽的多少之间的关系,在不同的温差下统计了100颗小麦种子的发芽数,得到了如下数据:
温差 | 8 | 10 | 11 | 12 | 13 |
发芽数 | 79 | 81 | 85 | 86 | 90 |
(1)请根据统计的最后三组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若由(1)中的线性回归方程得到的估计值与前两组数据的实际值误差均不超过两颗,则认为线性回归方程是可靠的,试判断(1)中得到的线性回归方程是否可靠;
(3)若100颗小麦种子的发芽率为![]() 颗,则记为
颗,则记为![]() 的发芽率,当发芽率为
的发芽率,当发芽率为![]() 时,平均每亩地的收益为
时,平均每亩地的收益为![]() 元,某农场有土地10万亩,小麦种植期间昼夜温差大约为
元,某农场有土地10万亩,小麦种植期间昼夜温差大约为![]() ,根据(1)中得到的线性回归方程估计该农场种植小麦所获得的收益.
,根据(1)中得到的线性回归方程估计该农场种植小麦所获得的收益.
附:在线性回归方程![]() 中,
中,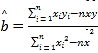 .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】在△![]() 中,角
中,角![]() 、
、![]() 、
、![]() 所对的边分别为
所对的边分别为![]() 、
、![]() 、
、![]() ,给出四个命题:
,给出四个命题:
(1)若![]() ,则△
,则△![]() 为等腰三角形;
为等腰三角形;
(2)若![]() ,则△
,则△![]() 为直角三角形;
为直角三角形;
(3)若![]() ,则△
,则△![]() 为等腰直角三角形;
为等腰直角三角形;
(4)若![]() ,则△
,则△![]() 为正三角形;
为正三角形;
以上正确命题的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】已知若椭圆![]() :
:![]() (
(![]() )交
)交![]() 轴于
轴于![]() ,
,![]() 两点,点
两点,点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() ,
,![]() 的任意一点,直线
的任意一点,直线![]() ,
,![]() 分别交
分别交![]() 轴于点
轴于点![]() ,
,![]() ,则
,则![]() 为定值
为定值![]() .
.
(1)若将双曲线与椭圆类比,试写出类比得到的命题;
(2)判定(1)类比得到命题的真假,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市居民自来水收费标准如下:每户每月用水不超过4吨时,每吨为![]() 元,当用水超过4吨时,超过部分每吨为
元,当用水超过4吨时,超过部分每吨为![]() 元,每月甲、乙两户共交水费
元,每月甲、乙两户共交水费![]() 元,已知甲、乙两户该月用水量分别为
元,已知甲、乙两户该月用水量分别为![]() .
.
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若甲、乙两户该月共交水费![]() 元,分别求出甲、乙两户该月的用水量.
元,分别求出甲、乙两户该月的用水量.
查看答案和解析>>
科目: 来源: 题型:
【题目】祖暅(公元前5~6世纪)是我国齐梁时代的数学家,是祖冲之的儿子,他提出了一条原原理:“幂势既同,则积不容异.”这里的“幂”指水平截面的面积,“势”指高。这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体体积相等。设由椭圆![]() 所围成的平面图形绕
所围成的平面图形绕![]() 轴旋转一周后,得一橄榄状的几何体(称为椭球体),课本中介绍了应用祖暅原理求球体体积公式的做法,请类比此法,求出椭球体体积,其体积等于( )
轴旋转一周后,得一橄榄状的几何体(称为椭球体),课本中介绍了应用祖暅原理求球体体积公式的做法,请类比此法,求出椭球体体积,其体积等于( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com