科目： 来源： 题型：
【题目】设数列{an}的前n项和为Sn，a1＝3，且Sn＝nan＋1－n2－n．
（1）求{an}的通项公式；
（2）若数列{bn}满足
，求{bn}的前n项和Tn．
查看答案和解析>>
科目： 来源： 题型：
【题目】袋子中有四个小球，分别写有“美、丽、中、国”四个字，有放回地从中任取一个小球，直到“中”“国”两个字都取到就停止，用随机模拟的方法估计恰好在第三次停止的概率．利用电脑随机产生0到3之间取整数值的随机数，分别用0，1，2，3代表“中、国、美、丽”这四个字，以每三个随机数为一组，表示取球三次的结果，经随机模拟产生了以下18组随机数：
232 321 230 023 123 021 132 220 001
231 130 133 231 031 320 122 103 233
由此可以估计，恰好第三次就停止的概率为
A. 
B. 
C. 
D. 
查看答案和解析>>
科目： 来源： 题型：
【题目】已知一扇形的圆心角为α，半径为R，弧长为l.
(1)若α＝60°，R＝10 cm，求扇形的弧长l；
(2)已知扇形的周长为10 cm，面积是4 cm2，求扇形的圆心角；
(3)若扇形周长为20 cm，当扇形的圆心角α为多少弧度时，这个扇形的面积最大？
查看答案和解析>>
科目： 来源： 题型：
【题目】如图1为某省2018年1~4月快递业务量统计图，图2是该省2018年1~4月快递业务收入统计图，下列对统计图理解错误的是（ ）
A. 2018年1~4月的业务量，3月最高，2月最低，差值接近2000万件
B. 2018年1~4月的业务量同比增长率均超过50%，在3月底最高
C. 从两图来看，2018年1~4月中的同一个月的快递业务量与收入的同比增长率并不完全一致
D. 从1~4月来看，该省在2018年快递业务收入同比增长率逐月增长
查看答案和解析>>
科目： 来源： 题型：
【题目】（选修4-4：坐标系与参数方程）
已知曲线C的极坐标方程是ρ=2cosθ，以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线L的参数方程是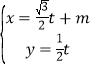
（t为参数）．
（1）求曲线C的直角坐标方程和直线L的普通方程；
（2）设点P（m，0），若直线L与曲线C交于A，B两点，且|PA||PB|=1，求实数m的值．
查看答案和解析>>
科目： 来源： 题型：
【题目】给出下列命题：
①已知
，
是正数，且
，则
；
②命题“
，使得
”的否定是真命题；
③将
化成二进位制数是
；
④某同学研究变量
，
之间的相关关系，并求得回归直线方程，他得出一个结论：与 负相关且
，
其中正确的命题的序号是__________(把你认为正确的序号都填上).
查看答案和解析>>
科目： 来源： 题型：
【题目】某学校为了解高三复习效果，从高三第一学期期中考试成绩中随机抽取50名考生的数学成绩，分成6组制成频率分布直方图如图所示：
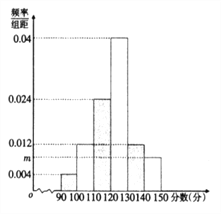
（1）求
的值及这50名同学数学成绩的平均数
；
（2）该学校为制定下阶段的复习计划，从成绩在
的同学中选出3位作为代表进行座谈，若已知成在
的同学中男女比例为2：1，求至少有一名女生参加座谈的概率.
查看答案和解析>>
科目： 来源： 题型：
【题目】在平面直角坐标系
中，曲线
的参数方程是
(
为参数)，以原点
为极点， 
轴正半轴为极轴，建立极坐标系，直线
的极坐标方程为
.
(Ⅰ)求曲线
的普通方程与直线
的直角坐标方程；
(Ⅱ)已知直线
与曲线
交于
， 
两点，与
轴交于点
，求
.
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，在三棱锥P-ABC中，已知PC⊥BC，PC⊥AC，点E，F，G分别是所在棱的中点，则下面结论中错误的是 ( )
A.平面EFG∥平面PBC
B.平面EFG⊥平面ABC
C.∠BPC是直线EF与直线PC所成的角
D.∠FEG是平面PAB与平面ABC所成二面角的平面角
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
