A. 一枚硬币掷两次,A=“第一次为正面向上”,B=“第二次为反面向上”

B. 袋中有两个白球和两个黑球,不放回地摸两球,A=“第一次摸到白球”,B=“第二次摸到白球”

C. 掷一枚骰子,A=“出现点数为奇数”,B=“出现点数为偶数”

D. A=“人能活到20岁”,B=“人能活到50岁”

(1)问捕捞几年后总盈利最大，最大是多少？

(2)问捕捞几年后的平均利润最大，最大是多少？

【题目】共享单车是城市慢行系统的一种创新模式，对于解决民众出行“最后一公里”的问题特别见效，由于停取方便、租用价格低廉，各色共享单车受到人们的热捧．某自行车厂为共享单车公司生产新样式的单车，已知生产新样式单车的固定成本为20 000元，每生产一辆新样式单车需要增加投入100元．根据初步测算，自行车厂的总收益(单位：元)满足分段函数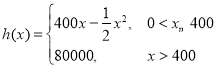 其中x是新样式单车的月产量(单位：辆)，利润＝总收益－总成本．

(1)试将自行车厂的利润y元表示为月产量x的函数；

(2)当月产量为多少件时自行车厂的利润最大？最大利润是多少？

【题目】一次数学测验中，全班名学生的数学成绩的频率分布直方图如下，已知分数在的学生数有14人.

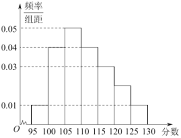
（1）求总人数和分数在的人数；

（2）利用频率分布直方图，估算该班学生数学成绩的众数和中位数，平均数各是多少？

【题目】已知点、为双曲线的左、右焦点，过作垂直于轴的直线，在轴上方交双曲线于点，且，圆的方程是.

（1）求双曲线的方程；

（2）过双曲线上任意一点作该双曲线两条渐近线的垂线，垂足分别为、，求的值；

（3）过圆上任意一点作圆的切线交双曲线于、两点，中点为，求证：

【题目】已知数列的首项为1.记.

（1）若为常数列，求的值：

（2）若为公比为2的等比数列，求的解析式：

（3）是否存在等差数列，使得对一切都成立？若存在，求出数列的通项公式：若不存在，请说明理由.

【题目】已知函数 ，其中.

（Ⅰ）讨论的单调性；

（Ⅱ）若存在使得，求实数的取值范围；

（Ⅲ）若当时恒有，求实数的取值范围.

【题目】如图，在四棱锥中，底面为平行四边形，，，，平面平面，点为上一点．

（1）若平面，求证：点为中点；

（2）求证：平面平面．

【题目】已知动点到点的距离，等于它到直线的距离．

(1)求点的轨迹的方程；

（2）过点任意作互相垂直的两条直线，分别交曲线于点和．

设线段，的中点分别为，求证：直线恒过一个定点；

（3）在（2）的条件下，求面积的最小值

【题目】2018年8月31日，十三届全国人大常委会第五次会议表决通过了关于修改个人所得税法的决定，这是我国个人所得税法自1980年出台以来第七次大修为了让纳税人尽早享受减税红利，在过渡期对纳税个人按照下表计算个人所得税，值得注意的是起征点变为5000元，即如表中“全月应纳税所得额”是纳税者的月薪金收入减去5000元后的余额．

某企业员工今年10月份的月工资为15000元，则应缴纳的个人所得税为______元