科目： 来源：北京模拟题 题型：单选题

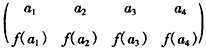已知集合A={l，2，3，4}，函数f(x)的定义域、值域都是A，且对于任意i∈A，f(i)≠i，设a₁，a₂，a₃，a₄是1，2，3，4的任意一个排列，定义数表，若两个数表的对应位置上至少有一个数不同，就说这是两张不同的数表，那么满足条件的不同的数表的张数为

[     ]

A．216
B．108
C．48
D．24

科目： 来源：模拟题 题型：解答题

如图所示，某学校要用鲜花布置花圃中A、B、C、D、E五个不同区域，要求同一区域上用同一种颜色的鲜花，相邻区域使用不同颜色的鲜花，现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择。

（1）当A、D区域同时用红色鲜花时，求布置花圃的不同方法的种数；
（2）求恰有两个区域用红色鲜花的概率；
（3）记ξ为花圃中用红色鲜花布置的区域的个数，求随机变量ξ的分布列及其数学期望Eξ。

科目： 来源：四川省高考真题 题型：单选题

科目： 来源：辽宁省高考真题 题型：单选题

科目： 来源：天津高考真题 题型：填空题

科目： 来源：陕西省高考真题 题型：填空题

科目： 来源：浙江省高考真题 题型：填空题

科目： 来源：湖南省高考真题 题型：单选题

科目： 来源：四川省高考真题 题型：填空题

科目： 来源：辽宁省高考真题 题型：单选题