
科目: 来源: 题型:
【题目】正四棱锥P﹣ABCD的底面边长为2,侧棱长为2![]() ,过点A作一个与侧棱PC垂直的平面α,则平面α被此正四棱锥所截的截面面积为_____,平面α将此正四棱锥分成的两部分体积的比值为_____.
,过点A作一个与侧棱PC垂直的平面α,则平面α被此正四棱锥所截的截面面积为_____,平面α将此正四棱锥分成的两部分体积的比值为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知定点![]() (
(![]() 为正常数),
为正常数),![]() 为
为![]() 轴负半轴上的一个动点,动点
轴负半轴上的一个动点,动点![]() 满足
满足![]() ,且线段
,且线段![]() 的中点在
的中点在![]() 轴上.
轴上.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设![]() 为曲线
为曲线![]() 的一条动弦(
的一条动弦(![]() 不垂直于
不垂直于![]() 轴).其垂直平分线与
轴).其垂直平分线与![]() 轴交于点
轴交于点![]() .当
.当![]() 时,求
时,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
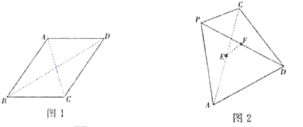
【题目】已知四边形![]() 是边长为5的菱形,对角线
是边长为5的菱形,对角线![]() (如图1),现以
(如图1),现以![]() 为折痕将菱形折起,使点
为折痕将菱形折起,使点![]() 达到点
达到点![]() 的位置.棱
的位置.棱![]() ,
,![]() 的中点分为
的中点分为![]() ,
,![]() ,且四面体
,且四面体![]() 的外接球球心落在四面体内部(如图2),则线段
的外接球球心落在四面体内部(如图2),则线段![]() 长度的取值范围为( )
长度的取值范围为( )
A.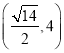 B.
B.![]() C.
C.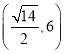 D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,左右顶点分别为
,左右顶点分别为![]() ,
,![]() ,上顶点为
,上顶点为![]() ,
,![]()
(1)求椭圆离心率;
(2)点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求椭圆方程;
,求椭圆方程;
(3)在(2)的条件下,点![]() 在椭圆上且异于
在椭圆上且异于![]() 、
、![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,说明
,说明![]() 运动时以
运动时以![]() 为直径的圆与直线
为直径的圆与直线![]() 的位置关系,并证明.
的位置关系,并证明.
查看答案和解析>>
科目: 来源: 题型:
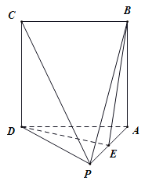
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,正方形
,正方形![]() 边长为2,
边长为2,![]() 是
是![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的长度;
的长度;
(3)若![]() ,线段
,线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 平面
平面![]() ,若存在求
,若存在求![]() 的长度,若不存在则说明.
的长度,若不存在则说明.
查看答案和解析>>
科目: 来源: 题型:
【题目】2020年1月1日《天津日报》发表文章总结天津海河英才计划成果“厚植热土 让天下才天津用”——我市精细服务海河英才优化引才结构.“海河英才”行动计划,紧紧围绕“一基地三区”定位,聚焦战略性新兴产业人才需求,大力、大胆集聚人才.政策实施1年半以来,截至2019年11月30日,累计引进各类人才落户23.5万人.具体比例如图所示,新引进两院院士,长江学者,杰出青年科学基金获得者等顶尖领军人才112人.记者李军计划从人才库中随机选取一部分英才进行跟踪调查采访.
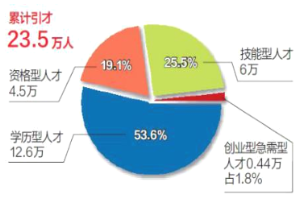
(1)李军抽取了8人其中学历型人才4人,技能型人才3人,资格型人才1人,周二和周五随机进行采访,每天4人(4人顺序任意),周五采访学历型人才人数不超过2人的概率;
(2)李军抽取不同类型的人才有不同的采访补贴,学历型人才500元/人,技能型人才400元/人,资格型人才600元/人,则创业型急需型人才最少补贴多少元/人使每名人才平均采访补贴费用大于等于500元/人?
查看答案和解析>>
科目: 来源: 题型:
【题目】对于数列![]() ,若存在
,若存在![]() ,使得
,使得![]() 对任意
对任意![]() 都成立,则称数列
都成立,则称数列![]() 为“
为“![]() 折叠数列”.
折叠数列”.
(1)若![]() ,
,![]() ,判断数列
,判断数列![]() ,
,![]() 是否是“
是否是“![]() 折叠数列”,如果是,指出m的值;如果不是,请说明理由;
折叠数列”,如果是,指出m的值;如果不是,请说明理由;
(2)若![]() ,求所有的实数q,使得数列
,求所有的实数q,使得数列![]() 是3-折叠数列;
是3-折叠数列;
(3)给定常数![]() ,是否存在数列
,是否存在数列![]() 使得对所有
使得对所有![]() ,
,![]() 都是
都是![]() 折叠数列,且
折叠数列,且![]() 的各项中恰有
的各项中恰有![]() 个不同的值,证明你的结论.
个不同的值,证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,短轴长为2,过定点
,短轴长为2,过定点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于不同的两点
于不同的两点![]() 、
、![]() (点
(点![]() 在点
在点![]() ,
,![]() 之间).
之间).
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)若射线![]() 交椭圆
交椭圆![]() 于点
于点![]() (
(![]() 为原点),求
为原点),求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂在制造产品时需要用到长度为698mm的A型和长度为518mm的B型两种钢管,工厂利用长度为4000mm的钢管原材料,裁剪成若干A型和B型钢管。假设裁剪时损耗忽略不计,裁剪后所剩废料与原材料的百分比称为废料率.
(1)有两种裁剪方案的废料率小于4.5%,请说明这两种方案并计算它们的废料率;
(2)工厂现有100根原材料钢管,一根A型和一根B型钢管为一套毛胚。按(1)中的方案裁剪,最多可裁剪多少套毛胚?最终的废料率为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com