
科目: 来源: 题型:
【题目】数列![]() 的数列
的数列![]() 的首项
的首项![]() ,前n项和为
,前n项和为![]() ,若数列
,若数列![]() 满足:对任意正整数n,k,当
满足:对任意正整数n,k,当![]() 时,
时,![]() 总成立,则称数列
总成立,则称数列![]() 是“
是“![]() 数列”
数列”
(1)若![]() 是公比为2的等比数列,试判断
是公比为2的等比数列,试判断![]() 是否为“
是否为“![]() ”数列?
”数列?
(2)若![]() 是公差为d的等差数列,且是“
是公差为d的等差数列,且是“![]() 数列”,求实数d的值;
数列”,求实数d的值;
(3)若数列![]() 既是“
既是“![]() ”,又是“
”,又是“![]() ”,求证:数列
”,求证:数列![]() 为等差数列.
为等差数列.
查看答案和解析>>
科目: 来源: 题型:
【题目】己知椭圆![]() 的离心率为
的离心率为![]() ,点
,点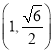 在椭圆C上.
在椭圆C上.
(1)求椭圆C的标准方程;
(2)过坐标原点的直线交C于P,Q两点,点P在第一象限,![]() 轴,垂足为E,连结QE并延长交C于点G.
轴,垂足为E,连结QE并延长交C于点G.
①求证:![]() 是直角三角形;
是直角三角形;
②求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】植物园拟建一个多边形苗圃,苗圃的一边紧靠着长度大于30m的围墙.现有两种方案:
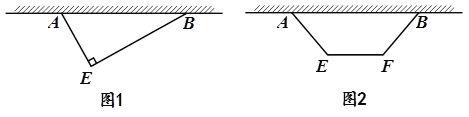
方案① 多边形为直角三角形![]() (
(![]() ),如图1所示,其中
),如图1所示,其中![]() ;
;
方案② 多边形为等腰梯形![]() (
(![]() ),如图2所示,其中
),如图2所示,其中![]() .
.
请你分别求出两种方案中苗圃的最大面积,并从中确定使苗圃面积最大的方案.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=|x﹣a|﹣|x﹣5|.
(1)当a=2时,求证:﹣3≤f(x)≤3;
(2)若关于x的不等式f(x)≤x2﹣8x+20在R恒成立,求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】根据某地区气象水文部门长期统计,可知该地区每年夏季有小洪水的概率为0.25,有大洪水的概率为0.05.
(1)从该地区抽取的![]() 年水文资料中发现,恰好3年无洪水事件的概率与恰好4年有洪水事件的概率相等,求
年水文资料中发现,恰好3年无洪水事件的概率与恰好4年有洪水事件的概率相等,求![]() 的值;
的值;
(2)今年夏季该地区某工地有许多大型设备,遇到大洪水时要损失60000元,遇到小洪水时要损失20000元.为保护设备,有以下3种方案:
方案1:修建保护围墙,建设费为3000元,但围墙只能防小洪水.
方案2:修建保护大坝,建设费为7000元,能够防大洪水.
方案3:不采取措施.
试比较哪一种方案好,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 为平面上一点,
为平面上一点,![]() 为直线
为直线![]() :
:![]() 上任意一点,过点
上任意一点,过点![]() 作直线
作直线![]() 的垂线
的垂线![]() ,设线段
,设线段![]() 的中垂线与直线
的中垂线与直线![]() 交于点
交于点![]() ,记点
,记点![]() 的轨迹为
的轨迹为![]() .
.
(1)求轨迹![]() 的方程;
的方程;
(2)过点![]() 作互相垂直的直线
作互相垂直的直线![]() 与
与![]() ,其中直线
,其中直线![]() 与轨迹
与轨迹![]() 交于点
交于点![]() 、
、![]() ,直线
,直线![]() 与轨迹
与轨迹![]() 交于点
交于点![]() 、
、![]() ,设点
,设点![]() ,
,![]() 分别是
分别是![]() 和
和![]() 的中点,求
的中点,求![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在数学中有这样形状的曲线:![]() .关于这种曲线,有以下结论:
.关于这种曲线,有以下结论:
①曲线![]() 恰好经过9个整点(即横、纵坐标均为整数的点);
恰好经过9个整点(即横、纵坐标均为整数的点);
②曲线![]() 上任意两点之间的距离都不超过2;
上任意两点之间的距离都不超过2;
③曲线![]() 所围成的“花瓣”形状区域的面积大于5.
所围成的“花瓣”形状区域的面积大于5.
其中正确的结论有:( )
A.①③B.②③C.①②D.①②③
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)![]() sin(ωx+φ)﹣cos(ωx+φ)(0<φ<π,ω>0)为偶函数,且y=f(x)图象的两相邻对称轴间的距离为
sin(ωx+φ)﹣cos(ωx+φ)(0<φ<π,ω>0)为偶函数,且y=f(x)图象的两相邻对称轴间的距离为![]() ,则f(
,则f(![]() )的值为( )
)的值为( )
A.﹣1B.1C.![]() .D.
.D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,曲线C的参数方程为
中,曲线C的参数方程为![]() (
(![]() 为参数),以原点O为极点,x轴正半轴为极轴建立极坐标系,直线
为参数),以原点O为极点,x轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,且直线
,且直线![]() 与曲线C有两个不同的交点.
与曲线C有两个不同的交点.
(1)求实数a的取值范围;
(2)已知M为曲线C上一点,且曲线C在点M处的切线与直线![]() 垂直,求点M的直角坐标.
垂直,求点M的直角坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com