
科目: 来源: 题型:
【题目】某社会机构为了调查对手机游戏的兴趣与年龄的关系,通过问卷调查,整理数据得如下![]() 列联表:
列联表:
40岁以下 | 40岁以上 | 合计 | |
很兴趣 | 30 | 15 | 45 |
无兴趣 | 20 | 35 | 55 |
合计 | 50 | 50 | 100 |
(1)根据列联表,能否有![]() 的把握认为对手机游戏的兴趣程度与年龄有关?
的把握认为对手机游戏的兴趣程度与年龄有关?
(2)若已经从![]() 岁以下的被调查者中用分层抽样的方式抽取了
岁以下的被调查者中用分层抽样的方式抽取了![]() 名,现从这
名,现从这![]() 名被调查者中随机选取
名被调查者中随机选取![]() 名,求这
名,求这![]() 名被调查者中恰有
名被调查者中恰有![]() 名对手机游戏无兴趣的概率.
名对手机游戏无兴趣的概率.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.84 | 6.635 | 10.828 |
(注:参考公式: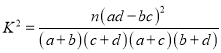 ,其中
,其中![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() 为直线
为直线![]() 的倾斜角),以坐标原点
的倾斜角),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的直角坐标方程,并求
的直角坐标方程,并求![]() 时直线
时直线![]() 的普通方程;
的普通方程;
(2)若直线![]() 和曲线
和曲线![]() 交于两点
交于两点![]() ,点
,点![]() 的直角坐标为
的直角坐标为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】程大位是明代著名数学家,他的《新编直指算法统宗》是中国历史上一部影响巨大的著作.卷八中第33问:“今有三角果一垛,底阔每面七个.问该若干?”如图是解决该问题的程序框图.执行该程序框图,求得该垛果子的总数S为( )

A.28B.56C.84D.120
查看答案和解析>>
科目: 来源: 题型:
【题目】平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为![]() (s为参数),以坐标原点为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(s为参数),以坐标原点为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() ,
,![]() ,直线与曲线C交于A,B两点.
,直线与曲线C交于A,B两点.
(Ⅰ)求直线l的普通方程和曲线C的直角坐标方程;
(Ⅱ)已知点P的极坐标为 ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与抛物线
与抛物线![]() 交于M,抛物线C的焦点为F,且
交于M,抛物线C的焦点为F,且![]() .
.
(Ⅰ)求抛物线C的方程;
(Ⅱ)设点Q是抛物线C上的动点,点D,E在y轴上,圆![]() 内切于三角形
内切于三角形![]() ,求三角形
,求三角形![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】目前,我国老年人口比例不断上升,造成日趋严峻的人口老龄化问题.2019年10月12日,北京市老龄办、市老龄协会联合北京师范大学中国公益研究院发布《北京市老龄事业发展报告(2018)》,相关数据有如下图表.规定年龄在15岁至59岁为“劳动年龄”,具备劳动力,60岁及以上年龄为“老年人”,据统计,2018年底北京市每2.4名劳动力抚养1名老年人.
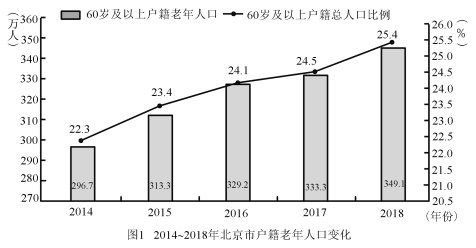
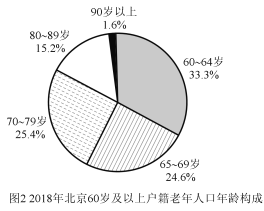
(Ⅰ)请根据上述图表计算北京市2018年户籍总人口数和北京市2018年的劳动力数;(保留两位小数)
(Ⅱ)从2014年起,北京市老龄人口与年份呈线性关系,比照2018年户籍老年人人口年龄构成,预计到2020年年底,北京市90以上老人达到多少人?(精确到1人)
(附:对于一组数据![]() 其回归直线
其回归直线![]() 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为: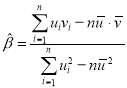 ,
,![]() .
.![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为![]() (s为参数),以坐标原点为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(s为参数),以坐标原点为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() ,
,![]() ,直线与曲线C交于A,B两点.
,直线与曲线C交于A,B两点.
(Ⅰ)求直线l的普通方程和曲线C的直角坐标方程;
(Ⅱ)已知点P的极坐标为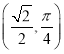 ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与抛物线
与抛物线![]() 交于M,抛物线C的焦点为F,且
交于M,抛物线C的焦点为F,且![]() .
.
(Ⅰ)求抛物线C的方程;
(Ⅱ)设点Q是抛物线C上的动点,点D,E在y轴上,圆![]() 内切于三角形
内切于三角形![]() ,求三角形
,求三角形![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com