
科目: 来源: 题型:
【题目】某中学举行了科学防疫知识竞赛.经过选拔,甲、乙、丙三位选手进入了最后角逐.他们还将进行四场知识竞赛.规定:每场知识竞赛前三名的得分依次为a,b,c(![]() ,且a,b,
,且a,b,![]() );选手总分为各场得分之和.四场比赛后,已知甲最后得分为16分,乙和丙最后得分都为8分,且乙只有一场比赛获得了第一名,则下列说法正确的是( )
);选手总分为各场得分之和.四场比赛后,已知甲最后得分为16分,乙和丙最后得分都为8分,且乙只有一场比赛获得了第一名,则下列说法正确的是( )
A.每场比赛的第一名得分a为4
B.甲至少有一场比赛获得第二名
C.乙在四场比赛中没有获得过第二名
D.丙至少有一场比赛获得第三名
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为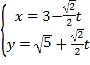 (
(![]() 为参数),在以坐标原点
为参数),在以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴的极坐标中,圆
轴正半轴为极轴的极坐标中,圆![]() 的方程为
的方程为![]() .
.
(1)写出直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 的坐标为
的坐标为![]() ,圆
,圆![]() 与直线
与直线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线PQ与⊙O相切于点A,AB是⊙O的弦,∠PAB的平分线AC交⊙O于点C,连结CB,并延长与直线PQ相交于点Q,若AQ=6,AC=5.
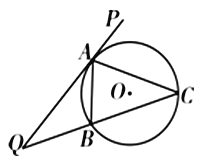
(Ⅰ)求证:QC2﹣QA2=BC![]() QC;
QC;
(Ⅱ)求弦AB的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在边长为4的菱形![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,将
,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如图2.
,如图2.

(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)判断在线段![]() 上是否存在一点
上是否存在一点![]() ,使平面
,使平面![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某厂商调查甲、乙两种不同型号电视机在10个卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图.
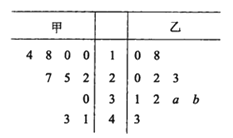
为了鼓励卖场,在同型号电视机的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”.
(1)当![]() 时,记甲型号电视机的“星级卖场”数量为
时,记甲型号电视机的“星级卖场”数量为![]() ,乙型号电视机的“星级卖场”数量为
,乙型号电视机的“星级卖场”数量为![]() ,比较
,比较![]() 的大小关系;
的大小关系;
(2)在这10个卖场中,随机选取2个卖场,记![]() 为其中甲型号电视机的“星级卖场”的个数,求
为其中甲型号电视机的“星级卖场”的个数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)若![]() ,记乙型号电视机销售量的方差为
,记乙型号电视机销售量的方差为![]() ,根据茎叶图推断
,根据茎叶图推断![]() 为何值时,
为何值时,![]() 达到最小值.(只需写出结论)
达到最小值.(只需写出结论)
查看答案和解析>>
科目: 来源: 题型:
【题目】某城市先后采用甲、乙两种方案治理空气污染各一年,各自随机抽取一年(365天)内100天的空气质量指数API的检测数据进行分析,若空气质量指数值在[0,300]内为合格,否则为不合格.表1是甲方案检测数据样本的频数分布表,如图是乙方案检测数据样本的频率分布直方图.
表1:
API值 | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | 大于300 |
天数 | 9 | 13 | 19 | 30 | 14 | 11 | 4 |
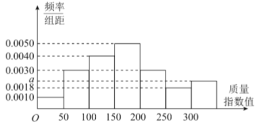
(1)将频率视为概率,求乙方案样本的频率分布直方图中![]() 的值,以及乙方案样本的空气质量不合格天数;
的值,以及乙方案样本的空气质量不合格天数;
(2)求乙方案样木的中位数;
(3)填写下面2×2列联表(如表2),并根据列联表判断是否有90%的把握认为该城市的空气质量指数值与两种方案的选择有关.
表2:
甲方案 | 乙方案 | 合计 | |
合格天数 | _______ | _______ | _______ |
不合格天数 | _______ | _______ | _______ |
合计 | _______ | _______ | _______ |
附: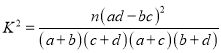
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目: 来源: 题型:
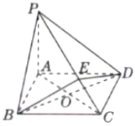
【题目】如图,在四棱锥![]() 中,ABCD为菱形,
中,ABCD为菱形,![]() 平面ABCD,连接AC,BD交于点O,
平面ABCD,连接AC,BD交于点O,![]() ,
,![]() ,E是棱PC上的动点,连接DE.
,E是棱PC上的动点,连接DE.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)当![]() 面积的最小值是4时,求此时点E到底面ABCD的距离.
面积的最小值是4时,求此时点E到底面ABCD的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com