【题目】已知函数，曲线在点处的切线在y轴上的截距为.

（1）求a；

（2）讨论函数和的单调性；

（3）设，求证：.

【题目】椭圆（）的离心率是，点在短轴上，且。

（1）球椭圆的方程；

（2）设为坐标原点，过点的动直线与椭圆交于两点。是否存在常数，使得为定值？若存在，求的值；若不存在，请说明理由。

【题目】某社区消费者协会为了解本社区居民网购消费情况，随机抽取了100位居民作为样本，就最近一年来网购消费金额(单位：千元)，网购次数和支付方式等进行了问卷调査.经统计这100位居民的网购消费金额均在区间内，按，，，，，分成6组，其频率分布直方图如图所示.

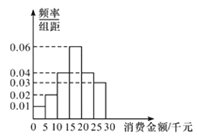
（1）估计该社区居民最近一年来网购消费金额的中位数；

（2）将网购消费金额在20千元以上者称为“网购迷”，补全下面的列联表，并判断有多大把握认为“网购迷与性别有关系”；

（3）调査显示，甲、乙两人每次网购采用的支付方式相互独立，两人网购时间与次数也互不. 影响.统计最近一年来两人网购的总次数与支付方式，所得数据如下表所示：

将频率视为概率，若甲、乙两人在下周内各自网购2次，记两人采用支付宝支付的次数之和为，求的数学期望.

附：观测值公式：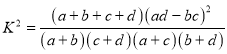

临界值表：

【题目】如图，在边长为的菱形中，，现沿对角线把翻折到的位置得到四面体，如图所示.已知.

（1）求证：平面平面；

（2）若是线段上的点，且，求二面角的余弦值.

【题目】在①，②（），③（）这三个条件中任选一个，补充在下面的问题中，若问题中的k存在，求出k的值；若k不存在，说明理由.已知数列为等比数列，，，数列的首项，其前n项和为，______，是否存在，使得对任意，恒成立？

注：如果选择多个条件分别解答，按第一个解答计分.

【题目】已知双曲线的左、右焦点分别为，实轴长为4，渐近线方程为，点N在圆上，则的最小值为( )

A. B. 5C. 6D. 7

【题目】南北朝时期的伟大数学家祖暅在数学上有突出贡献，他在实践的基础上提出祖暅原理：“幂势既同，则积不容异”.其含义是：夹在两个平行平面之间的两个几何体，被平行于这两个平行平面的任意平面所截，如果截得两个截面的面积总相等，那么这两个几何体的体积相等.如图，夹在两个平行平面之间的两个几何体的体积分别为、，被平行于这两个平面的任意平面截得的两个截面面积分别为、，则命题：“、相等”是命题“、总相等”的（ ）

A.充分不必要条件B.必要不充分条件

C.充要条件D.既不充分也不必要条件

【题目】如图，在三棱锥中，、、分别为棱、、的中点，平面，，，，则（ ）

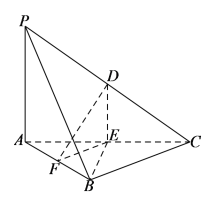
A.三棱锥的体积为

B.直线与直线垂直

C.平面截三棱锥所得的截面面积为

D.点与点到平面的距离相等

【题目】已知函数的最大值为，其图像相邻的两条对称轴之间的距离为，且的图像关于点对称，则下列结论正确的是（ ）.

A.函数的图像关于直线对称

B.当时，函数的最小值为

C.若，则的值为

D.要得到函数的图像，只需要将的图像向右平移个单位

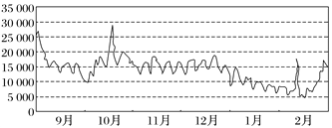
根据该走势图，下列结论不正确的是（ ）.

A.这半年中，网民对该关键词相关的信息关注度与时间具有比较明显的线性相关性

B.2019年10月网民对该关键词的搜索指数变化的走势图具有较好的对称性，与正态曲线相近，故当月搜索指数的平均值约为29000

C.从网民对该关键词的搜索指数来看，2019年10月的方差小于11月的方差

D.从网民对该关键词的搜索指数来看，2019年12月的平均值大于2020年1月的平均值