
科目: 来源: 题型:
【题目】《周易》是我国古代典籍,用“卦”描述了天地世间万象变化.如图是一个八卦图,包含乾、坤、震、巽、坎、离、艮、兑八卦(每一卦由三个爻组成,其中“![]() ”表示一个阳爻,“
”表示一个阳爻,“![]() ”表示一个阴爻).若从八卦中任取两卦,这两卦的六个爻中恰有一个阳爻的概率为( )
”表示一个阴爻).若从八卦中任取两卦,这两卦的六个爻中恰有一个阳爻的概率为( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
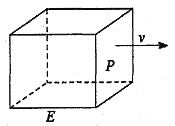
【题目】如图,长方形物体E在雨中沿面P(面积为S)的垂直方向作匀速移动,速度为![]() ,雨速沿E移动方向的分速度为
,雨速沿E移动方向的分速度为![]() 。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与
。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与![]() ×S成正比,比例系数为
×S成正比,比例系数为![]() ;(2)其它面的淋雨量之和,其值为
;(2)其它面的淋雨量之和,其值为![]() ,记
,记![]() 为E移动过程中的总淋雨量,当移动距离d=100,面积S=
为E移动过程中的总淋雨量,当移动距离d=100,面积S=![]() 时。
时。
(1)写出![]() 的表达式
的表达式
(2)设0<v≤10,0<c≤5,试根据c的不同取值范围,确定移动速度![]() ,使总淋雨量
,使总淋雨量![]() 最少。
最少。
查看答案和解析>>
科目: 来源: 题型:
【题目】(本小题共l4分)
已知函数f(x)=![]() x +
x +![]() , h(x)=
, h(x)=![]() .
.
(I)设函数F(x)=f(x)一h(x),求F(x)的单调区间与极值;
(Ⅱ)设a∈R,解关于x的方程log4[![]() ]=1og2h(a-x)一log2h (4-x);
]=1og2h(a-x)一log2h (4-x);
(Ⅲ)试比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知真命题:“函数![]() 的图象关于点
的图象关于点![]() 成中心对称图形”的充要条件为“函数
成中心对称图形”的充要条件为“函数![]() 是奇函数”.
是奇函数”.
(Ⅰ)将函数![]() 的图象向左平移1个单位,再向上平移2个单位,求此时图象对应的函数解析式,并利用题设中的真命题求函数
的图象向左平移1个单位,再向上平移2个单位,求此时图象对应的函数解析式,并利用题设中的真命题求函数![]() 图象对称中心的坐标;
图象对称中心的坐标;
(Ⅱ)求函数![]() 图象对称中心的坐标;
图象对称中心的坐标;
(Ⅲ)已知命题:“函数![]() 的图象关于某直线成轴对称图象”的充要条件为“存在实数
的图象关于某直线成轴对称图象”的充要条件为“存在实数![]() 和
和![]() ,使得函数
,使得函数![]() 是偶函数”.判断该命题的真假.如果是真命题,请给予证明;如果是假命题,请说明理由,并类比题设的真命题对它进行修改,使之成为真命题(不必证明).
是偶函数”.判断该命题的真假.如果是真命题,请给予证明;如果是假命题,请说明理由,并类比题设的真命题对它进行修改,使之成为真命题(不必证明).
查看答案和解析>>
科目: 来源: 题型:
【题目】某企业接到生产3000台某产品的![]() 三种部件的订单,每台产品需要这三种部件的数量分别为2,2,1(单位:件),已知每个工人每天可生产A部件6件,或B部件3件,或C部件2件.该企业计划安排200名工人分成三组分别生产这三种部件,生产B部件的人数与生产A部件的人数成正比,比例系数为k(k为正整数).
三种部件的订单,每台产品需要这三种部件的数量分别为2,2,1(单位:件),已知每个工人每天可生产A部件6件,或B部件3件,或C部件2件.该企业计划安排200名工人分成三组分别生产这三种部件,生产B部件的人数与生产A部件的人数成正比,比例系数为k(k为正整数).
(1)设生产![]() 部件的人数为
部件的人数为![]() ,分别写出完成
,分别写出完成![]() 三种部件生产需要的时间;
三种部件生产需要的时间;
(2)假设这三种部件的生产同时开工,试确定正整数k的值,使完成订单任务的时间最短,并给出时间最短时具体的人数分组方案.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=lg(x+1).
(1)若0<f(1-2x)-f(x)<1,求实数x的取值范围;
(2)若g(x)是以2为周期的偶函数,且当0≤x≤1时,有g(x)=f(x),当x∈[1,2]时,求函数y=g(x)的解析式.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=x22(a+2)x+a2,g(x)=x2+2(a2)xa2+8.设H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)}(max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记H1(x)的最小值为A,H2(x)的最大值为B,则AB=( )
A.a22a16B.a2+2a16
C.16D.16
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 的焦点
的焦点![]() 到准线
到准线![]() 的距离为2,直线
的距离为2,直线![]() 与抛物线交于不同的两点
与抛物线交于不同的两点![]() ,
,![]() .
.
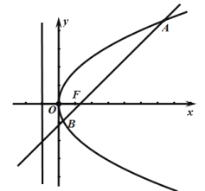
(1)求抛物线的方程;
(2)是否存在与![]() 的取值无关的定点
的取值无关的定点![]() ,使得直线
,使得直线![]() ,
,![]() 的斜率之和恒为定值?若存在,求出所有点
的斜率之和恒为定值?若存在,求出所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com