
科目: 来源:期末题 题型:单选题
查看答案和解析>>
科目: 来源:同步题 题型:单选题
 =(a1,a2,a3,a4,…,an),
=(a1,a2,a3,a4,…,an), =(b1,b2,
=(b1,b2, 与
与 夹角θ的余弦为cosθ=
夹角θ的余弦为cosθ= .已知n维向量
.已知n维向量 ,
, ,当
,当 =(1,1,1,1,…,1),
=(1,1,1,1,…,1), =(﹣1,﹣1,1,1,1,…,1)时,cosθ等于
=(﹣1,﹣1,1,1,1,…,1)时,cosθ等于



查看答案和解析>>
科目: 来源:高考真题 题型:填空题

查看答案和解析>>
科目: 来源:高考真题 题型:解答题
查看答案和解析>>
科目: 来源:期末题 题型:填空题
查看答案和解析>>
科目: 来源:高考真题 题型:单选题
 ,人们还用过一些类似的近似公式.根据x=3.14159…..判断,下列近似公式中最精确的一个是
,人们还用过一些类似的近似公式.根据x=3.14159…..判断,下列近似公式中最精确的一个是



查看答案和解析>>
科目: 来源:高考真题 题型:单选题
查看答案和解析>>
科目: 来源:月考题 题型:填空题
请阅读下列材料:
若两个正实数a1,a2满足a12+a22=1,那么a1+a2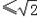 .证明:构造函数
.证明:构造函数
f(x)=(x﹣a1)2+(x﹣a2)2=2x2﹣2(a1+a2)x+1,因为对一切实数x,恒有f(x)≥0,所以△≤0,从而得4(a1+a2)2﹣8≤0,所以a1+a2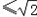 .
.
根据上述证明方法,若n个正实数满足a12+a22+…+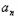 2=1时,你能得到的结论为( )
2=1时,你能得到的结论为( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com