练习册

  • 练习册
  • 试题
    相关习题
     0  28965  28973  28979  28983  28989  28991  28995  29001  29003  29009  29015  29019  29021  29025  29031  29033  29039  29043  29045  29049  29051  29055  29057  29059  29060  29061  29063  29064  29065  29067  29069  29073  29075  29079  29081  29085  29091  29093  29099  29103  29105  29109  29115  29121  29123  29129  29133  29135  29141  29145  29151  29159  266669 

    科目： 来源： 题型：

    已知函数f（x）=ax-3，g（x）=bx-1+cx-2（a，b∈R）且g(-
    12
    )-g(1)=f(0)    ．
    （1）试求b，c所满足的关系式；
    （2）若b=0，方程f（x）=g（x）在（0，+∞）有唯一解，求a的取值范围；
    （3）若b=1，集合A={x|f（x）＞g（x），g（x）＜0}，试求集合A；

    查看答案和解析>>

    科目： 来源： 题型：

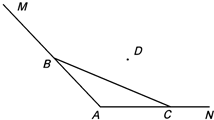    精英家教网如图，海岸线MAN，∠A=2θ，现用长为l的拦网围成一养殖场，其中B∈MA，C∈NA．
    （1）若BC=l，求养殖场面积最大值；
    （2）若B、C为定点，BC＜l，在折线MBCN内选点D，使BD+DC=l，求四边形养殖场DBAC的最大面积．

    查看答案和解析>>

    科目： 来源： 题型：

    设数列S1，S2，…是一个严格递增的正整数数列．
    （1）若SSk+1，SSk+1是该数列的其中两项，求证：SSk+1≤SSk+1；
    （2）若该数列的两个子数列SS1，SS2…和SS1+1，SS2+1，…都是等差数列，求证：这两个子数列的公差相等；
    （3）若（2）中的公差为1，求证：SSk+1≥SSk+1，并证明数列{Sn}也是等差数列．

    查看答案和解析>>

    科目： 来源： 题型：

    已知等差数列{an}的首项为a，公差为b，等比数列{bn}的首项为b，公比为a（其中a，b均为正整数）．
    （Ⅰ）若a1=b1，a2=b2，求数列{an}、{bn}的通项公式；
    （Ⅱ）在（Ⅰ）的条件下，若a1，a3，an1，an2，…，ank，…（3＜n1＜n2＜…＜nk＜…）成等比数列，求数列{nk}的通项公式；
    （Ⅲ）若a1＜b1＜a2＜b2＜a3，且至少存在三个不同的b值使得等式am+t=bn（t∈N）成立，试求a、b的值．

    查看答案和解析>>

    科目： 来源： 题型：

    已知数列{an}的前n项和为Sn，数列{
    		Sn+1
    }    是公比为2的等比数列．
    （1）证明：数列{an}成等比数列的充要条件是a1=3；
    （2）设bn=5n-（-1）nan（n∈N*）．若bn＜bn+1对n∈N*恒成立，求a1的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：

    20、已知等差数列{an}的首项为a，公差为b，等比数列{bn}的首项为b，公比为a，其中a，b都是大于1
    的正整数，且a1＜b1，b2＜a3．
    （1）求a的值；
    （2）若对于任意的n∈N+，总存在m∈N+，使得am+3=bn成立，求b的值；
    （3）令Cn=an+1+bn，问数列{Cn}中是否存在连续三项成等比数列？若存在，求出所有成等比数列的连续三项；若不存在，请说明理由．

    查看答案和解析>>

    科目： 来源： 题型：

    函数f（x）=x3-3x．
    （1）求函数f（x）的极值；
    （2）已知f（x）在[t，t+2]上是增函数，求t的取值范围；
    （3）f（x）在[t，t+2]上最大值M与最小值m之差M-m为g（t），求g（t）的最小值．

    查看答案和解析>>

    科目： 来源： 题型：

    已知函数f（x）=x2-4x+（2-a）lnx，（a∈R，a≠0）．
    （1）当a=8时，求函数f（x）的单调区间；
    （2）求函数f（x）在区间[e，e2]上的最小值．

    查看答案和解析>>

    科目： 来源： 题型：

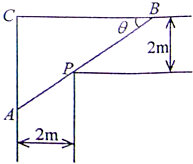    精英家教网某直角走廊的示意图如图所示，其两边走廊的宽度均为2m．
    （1）过点p的一条直线与走廊的外侧两边交于A，B两点，且与走廊的一边的夹角为θ(0＜θ＜
    π2
    )    ，将线段AB的长度l表示为θ的函数；
    （2）一根长度为5m的铁棒能否水平（铁棒与地面平行）通过该直角走廊？请说明理由（铁棒的粗细忽略不计）．

    查看答案和解析>>

    科目： 来源： 题型：

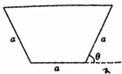    精英家教网汶川大地震后，为了消除某堰塞湖可能造成的危险，救授指挥部商定，给该堰塞湖挖一个横截面为等腰梯形的简易引水槽（如图所示）进行引流，已知等腰梯形的下底与腰的长度都为a，且水槽的单位时间内的最大流量与横载面的面积为正比，比例系数k＞0．
    （1）试将水槽的最大流量表示成关于θ的函数f（θ）；
    （2）为确保人民的生命财产安全，请你设计一个方案，使单位时间内水槽的流量最大（即当θ为多大时，单位时间内水槽的流量最大）．

    查看答案和解析>>

    同步练习册答案