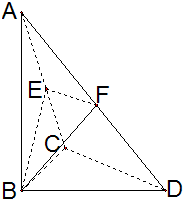如图，已知△BCD中，∠BCD=90°，AB⊥平面BCD，BC=CD=1，AB=

3

，E、F分别为AC、AD的中点．
（1）求证：平面BEF⊥平面ABC；
（2）求直线AD与平面BEF所成角的正弦值．

已知四面体A-BCD的棱长均为2，其正视图是边长为2的等边三角形（如图，其中BC为水平线），则其侧视图的面积是．

A、 13

B、8

C、16

D、8 2

已知直线x-2y+4=0经过椭圆C：

x2

a2

+

y2

b2

=1(a＞b＞0)的左顶点A和上顶点D，椭圆C的右顶点为B，点P是椭圆C上位于x轴上方的动点，直线AP，BP与直线l：x=5分别交于M，N两点．
（1）求椭圆C的方程；
（2）求线段MN的长度的最小值；
（3）当线段MN的长度最小时，Q点在椭圆上运动，记△BPQ的面积为S，当S在（0，+∞）上变化时，讨论S的大小与Q点的个数之间的关系．

为了研究化肥对小麦产量的影响，某科学家将一片土地划分成200个50m²的小块，并在100个小块上施用新化肥，留下100个条件大体相当的小块不施用新化肥．下表1和表2分别是施用新化肥和不施用新化肥的小麦产量频数分布表（小麦产量单位：kg）
表1：施用新化肥小麦产量频数分布表

小麦产量	[0，10）	[10，20）	[20，30）	[30，40）	[40，50）
频数	10	35	40	10	5

表2：不施用新化肥小麦产量频数分布表

小麦产量	[0，10）	[10，20）	[20，30）	[30，40）
频数	15	50	30	5

（1）完成下面频率分布直方图；

施用新化肥后小麦产量的频率分布直方图       不施用新化肥后小麦产量的频率分布直方图
（2）统计方法中，同一组数据常用该组区间的中点值作为代表，据此估计施用化肥和不施用化肥的一小块土地的小麦平均产量；
（3）完成下面2×2列联表，并回答能否有99.5%的把握认为“施用新化肥和不施用新化肥的小麦产量有差异”
表3：

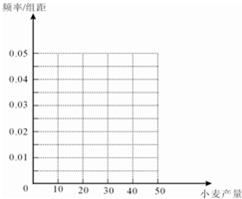
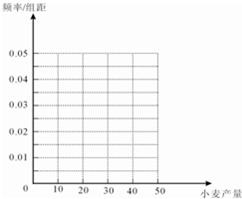
	小麦产量小于20kg	小麦产量不小于20kg	合计
施用新化肥	a=	b=
不施用新化肥	c=	d=
合计			n=

附：K2=

n(ad-bc)2

(a+b)(c+d)(a+c)(b+d)

P（K2≥k）	0.050     0.010     0.005      0.001
k	3.841     6.635     7.879     10.828

已知抛物线和双曲线都经过点M（1，2），它们在x轴上有共同焦点，双曲线的对称轴是坐标轴，抛物线的顶点为坐标原点．
（1）求这两条曲线的方程；
（2）直线l过x轴上定点N（异于原点），与抛物线交于A、B两点且以AB为直径的圆过原点，试求出定点N的坐标．

在每年的春节后，某市政府都会发动公务员参与到植树绿化活动中去．林业管理部门在植树前，为了保证树苗的质量，都会在植树前对树苗进行检测．现从甲、乙两种树苗中各抽测了10株树苗，量出它们的高度如下（单位：厘米）：
甲：37，21，31，20，29，19，32，23，25，33；
乙：10，30，47，27，46，14，26，10，44，46．
（1）画出两组数据的茎叶图，并根据茎叶图对甲、乙两种树苗的高度作比较，写出两个统计结论；
（2）设抽测的10株甲种树苗高度平均值为

.

x

，将这10株树苗的高度依次输入，按程序框（如图）进行运算，问输出的S大小为多少？并说明S的统计学意义．

已知p：|1-

x-1

2

|≤3，q：x2-2x+1-m2≤0（m＞0），若?p是?q的必要而不充分条件，求实数m的取值范围．

有下列四个命题：
①“若xy≠-1，则x≠1或y≠-1”是假命题；
②“?x∈R，x²+1＞1”的否定是“?x∈R，x²+1≤1”
③当a₁，a₂，b₁，b₂，c₁，c₂均不等于0时，“不等式a₁x²+b₁x+c₁＞0与a₂x²+b₂x+c₂＞0解集相同”是“

a1

a2

=

b1

b2

=

c1

c2

”的充要条件；
④“全等三角形相似”的否命题是“全等三角形不相似”，其中正确命题的序号是．
（写出你认为正确的所有命题序号）