
科目: 来源: 题型:
查看答案和解析>>
科目: 来源: 题型:
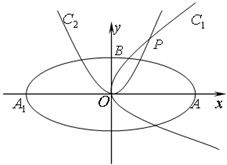 如图,椭圆C:
如图,椭圆C:| x2 |
| a2 |
| y2 |
| 2 |
| 2 |
| 2 |
| QM |
| QN |
查看答案和解析>>
科目: 来源: 题型:
| 1 | an•an+1 |
查看答案和解析>>
科目: 来源: 题型:
 某校高一年级共有学生320人.为调查高一年级学生每天晚自习自主支配学习时间(指除了完成教师布置的作业后学生根据自己的需要进行学习的时间)情况,学校采用随机抽样的方法从高一学生中抽取了n名学生进行问卷调查.根据问卷得到了这n名学生每天晚自习自主支配学习时间的数据(单位:分钟),按照以下区间分为七组:①[0,10),②[10,20),③[20,30),④[30,40),⑤[40,50),⑥[50,60),⑦[60,70),得到频率分布直方图如图.已知抽取的学生中每天晚自习自主支配学习时间低于20分钟的人数是4人.
某校高一年级共有学生320人.为调查高一年级学生每天晚自习自主支配学习时间(指除了完成教师布置的作业后学生根据自己的需要进行学习的时间)情况,学校采用随机抽样的方法从高一学生中抽取了n名学生进行问卷调查.根据问卷得到了这n名学生每天晚自习自主支配学习时间的数据(单位:分钟),按照以下区间分为七组:①[0,10),②[10,20),③[20,30),④[30,40),⑤[40,50),⑥[50,60),⑦[60,70),得到频率分布直方图如图.已知抽取的学生中每天晚自习自主支配学习时间低于20分钟的人数是4人.查看答案和解析>>
科目: 来源: 题型:
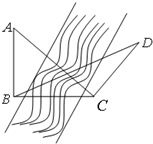
 如图,三棱柱ABC-A1B1C1中,BC⊥侧面AA1C1C,AC=BC=1,CC1=2,∠CAA1=
如图,三棱柱ABC-A1B1C1中,BC⊥侧面AA1C1C,AC=BC=1,CC1=2,∠CAA1=| π | 3 |
查看答案和解析>>
科目: 来源: 题型:
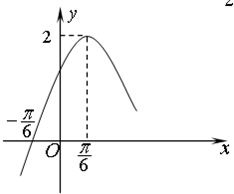 函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,0<φ<
函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,0<φ<| π |
| 2 |
| π |
| 12 |
| π |
| 6 |
| π |
| 3 |
查看答案和解析>>
科目: 来源: 题型:
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
查看答案和解析>>
科目: 来源: 题型:
 如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10米到位置D,测得∠BDC=45°,则塔AB的高是
如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10米到位置D,测得∠BDC=45°,则塔AB的高是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com