练习册

  • 练习册
  • 试题
    相关习题
     0  32657  32665  32671  32675  32681  32683  32687  32693  32695  32701  32707  32711  32713  32717  32723  32725  32731  32735  32737  32741  32743  32747  32749  32751  32752  32753  32755  32756  32757  32759  32761  32765  32767  32771  32773  32777  32783  32785  32791  32795  32797  32801  32807  32813  32815  32821  32825  32827  32833  32837  32843  32851  266669 

    科目： 来源： 题型：

    准线方程为x=1的抛物线的标准方程是（　　）
    A、y2=-2xB、y2=-4xC、y2=-2xD、y2=4x

    查看答案和解析>>

    科目： 来源： 题型：

    已知二次函数f（x）的二次项系数为a，满足不等式f（x）＞-2x的解集为（1，3），且方程f（x）+6a=0有两个相等实根，求f（x）的解析式．

    查看答案和解析>>

    科目： 来源： 题型：

    17、（1）已知实数a∈{-1，1，a2}，求方程x2-（1-a）x-2=0的解．

    查看答案和解析>>

    科目： 来源： 题型：

    3、函数y=f（x）的图象与一条直线x=a有交点个数是（　　）

    查看答案和解析>>

    科目： 来源： 题型：

    平面直角坐标系中，O为坐标原点，已知两点M（1，-3）、N（5，1），若点C满足
    OC
    =t
    OM
    +（1-t）
    ON
    （t∈R），点C的轨迹与抛物线：y2=4x交于A、B两点．
    （Ⅰ）求证：
    OA
    ⊥
    OB
    ；
    （Ⅱ）在x轴上是否存在一点P（m，0）（m∈R），使得过P点的直线交抛物线于D、E两点，并以该弦DE为直径的圆都过原点．若存在，请求出m的值及圆心的轨迹方程；若不存在，请说明理由．

    查看答案和解析>>

    科目： 来源： 题型：

    已知函数g(x)=
    1
    x•sinθ
    +lnx    在[1，+∞）上为增函数．且θ∈（0，π），f(x)=mx-
    m-1
    x
    -lnx (m∈R)
    （1）求θ的值；
    （2）若f（x）-g（x）在[1，+∞）函数是单调函数，求m的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：

    在数列{an}中，a1=2，an+1=an+2n+1（n∈N*）
    （1）求证：数列{an-2n}为等差数列；
    （2）设数列{bn}满足bn=log2（an+1-n），若(1+
    1
    b2
    )(1+
    1
    b3
    )(1+
    1
    b4
    )    …(1+
    1
    bn
    )＞k
    		n+1
    对一切n∈N*且n≥2恒成立，求实数k的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：

    已知函数f（x）=x3，g （x）=x+
    		x
    ．
    （Ⅰ）求函数h （x）=f（x）-g （x）的零点个数．并说明理由；
    （Ⅱ）设数列{ an}（n∈N*）满足a1=a（a＞0），f（an+1）=g（an），证明：存在常数M，使得对于任意的n∈N*，都有an≤M．

    查看答案和解析>>

    科目： 来源： 题型：

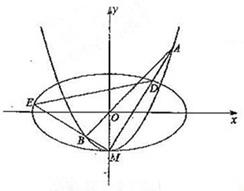    精英家教网如图，椭圆C1：
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0）的离心率为
    		3
    2
    ，x轴被曲线C2：y=x2-b截得的线段长等于C1的长半轴长．
    （Ⅰ）求C1，C2的方程；
    （Ⅱ）设C2与y轴的交点为M，过坐标原点O的直线l与C2相交于点A、B，直线MA，MB分别与C1相交于D，E．
    （i）证明：MD⊥ME；
    （ii）记△MAB，△MDE的面积分别是S1，S2．问：是否存在直线l，使得
    S1
    S2
    =
    17
    32
    ？请说明理由．

    查看答案和解析>>

    科目： 来源： 题型：

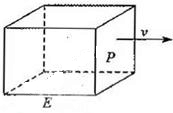    精英家教网如图，长方形物体E在雨中沿面P（面积为S）的垂直方向作匀速移动，速度为v（v＞0），雨速沿E移动方向的分速度为c（c∈R）．E移动时单位时间内的淋雨量包括两部分：（1）P或P的平行面（只有一个面淋雨）的淋雨量，假设其值与|v-c|×S成正比，比例系数为
    1
    10
    ；（2）其它面的淋雨量之和，其值为
    1
    2
    ，记y为E移动过程中的总淋雨量，当移动距离d=100，面积S=
    3
    2
    时．
    （Ⅰ）写出y的表达式
    （Ⅱ）设0＜v≤10，0＜c≤5，试根据c的不同取值范围，确定移动速度v，使总淋雨量y最少．

    查看答案和解析>>

    同步练习册答案