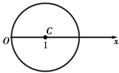如图，在极坐标系中，圆C的圆心坐标为（1，0），半径为1．
（Ⅰ）求圆C的极坐标方程；
（Ⅱ）若以极点O为原点，极轴所在直线为x轴建立平面直角坐标系．已知直线l的参数方程为

x=-1+tcos π 6 y=tsin π 6

（t为参数），试判断直线l与圆C的位置关系．

某同学用《几何画板》研究椭圆的性质：打开《几何画板》软件，绘制某椭圆C₁：

x2

a2

+

y2

b2

=1，在椭圆上任意画一个点S，度量点S的坐标（x_s，y_s），如图1．
（1）拖动点S，发现当x_s=

2

时，y_s=0；当x_s=0时，y_s=1，试求椭圆C₁的方程；
（2）该同学知圆具有性质：若E为圆O：x²+y²=r²（r＞0）的弦AB的中点，则直线AB的斜率k_AB与直线OE的斜率k_OE的乘积k_AB•k_OE为定值．该同学在椭圆上构造两个不同的点A、B，并构造直线AB，再构造AB的中点E，经观察得：沿着椭圆C₁，无论怎样拖动点A、B，椭圆也具有此性质．类比圆的这个性质，请写出椭圆C₁的类似性质，并加以证明；
（3）拖动点A、B的过程中，如图2发现当点A与点B在C₁在第一象限中的同一点时，直线AB刚好为C₁的切线l，若l分别与x轴和y轴的正半轴交于C，D两点，求三角形OCD面积的最小值．

已知函数f（x）=e^x，g（x）=lnx
（1）若曲线h（x）=f（x）+ax²-ex（a∈R）在点（1，h（1））处的切线垂直于y轴，求函数h（x）的单调区间；
（2）若函数F(x)=1-

a

x

-g(x) (a∈R)在区间（0，2）上无极值，求实数a的取值范围．

国Ⅳ标准规定：轻型汽车的氮氧化物排放量不得超过80mg/km．根据这个标准，检测单位从某出租车公司运营的A、B两种型号的出租车中分别抽取5辆，对其氮氧化物的排放量进行检测，检测结果记录如下（单位：mg/km）

A	85	80	85	60	90
B	70	x	95	y	75

由于表格被污损，数据x，y看不清，统计员只记得A、B两种出租车的氮氧化物排放量的平均值相等，方差也相等．
（1）求表格中x与y的值；
（2）从被检测的5辆B种型号的出租车中任取2辆，记“氮氧化物排放量超过80mg/km”的车辆数为ξ，求ξ的分布列和数学期望．

在某公司的开业周年庆典活动中，设有“幸运转盘”（如图所示）游戏项目，规定：①每位员工都有且只有一次转盘机会；②当指针位于区域Y（所对的圆心角为

π

2

）的时候，表示参与者获得“幸运大奖”．
（1）求某员工获得“幸运大奖”的概率；
（2）若某部门的3名员工依次参与游戏，记这3名员工中获得幸运大奖的员工人数为ξ，求ξ的分布列和数学期望．

（2010•福建模拟）考察等式：

C

0 m

C

r n-m

+

C

1 m

C

r-1 n-m

+…+

C

r m

C

0 n-m

=

C

r n

（*），其中n、m、r∈N^*，r≤m＜n且r≤n-m．某同学用概率论方法证明等式（*）如下：
设一批产品共有n件，其中m件是次品，其余为正品．现从中随机取出r件产品，
记事件A_k={取到的r件产品中恰有k件次品}，则P(Ak)=

C k m C r-k n-m

C r n

，k=0，1，2，…，r．
显然A₀，A₁，…，A_r为互斥事件，且A₀∪A₁∪…∪A_r=Ω（必然事件），
因此1=P（Ω）=P（A₀）+P（A₁）+…P（A_r）=

C 0 m C r n-m + C 1 m C r-1 n-m +…+ C r m C 0 n-m

C r n

，
所以

C

0 m

C

r n-m

+

C

1 m

C

r-1 n-m

+…+

C

r m

C

0 n-m

=

C

r n

，即等式（*）成立．
对此，有的同学认为上述证明是正确的，体现了偶然性与必然性的统一；但有的同学对上述证明方法的科学性与严谨性提出质疑．现有以下四个判断：
①等式（*）成立  ②等式（*）不成立  ③证明正确  ④证明不正确
试写出所有正确判断的序号．

甲乙两人进行乒乓球比赛，先赢三局者获胜，决出胜负为止，若各人输赢局次的不同视为不同情形，则甲胜的情形共有种（数字作答）．

袋中装有3个红球和2个白球，如果不放回依次抽取两次，记A={第一次抽到红球}，B={第二次抽到红球}，求p（B|A）=．

在二项式(

x

+2)6的展开式中，x²的系数是．

（2012•安徽模拟）设函数F(x)=

f(x)

ex

是定义在R上的函数，其中f（x）的导函数f′（x）满足f′（x）＜f（x）对于x∈R恒成立，则（　　）