练习册

  • 练习册
  • 试题
    相关习题
     0  37330  37338  37344  37348  37354  37356  37360  37366  37368  37374  37380  37384  37386  37390  37396  37398  37404  37408  37410  37414  37416  37420  37422  37424  37425  37426  37428  37429  37430  37432  37434  37438  37440  37444  37446  37450  37456  37458  37464  37468  37470  37474  37480  37486  37488  37494  37498  37500  37506  37510  37516  37524  266669 

    科目： 来源： 题型：

    （2013•崇明县二模）已知数列{an}是各项均不为0的等差数列，公差为d，Sn为其前n项和，且满足an2=S2n-1，n∈N*．数列{bn}满足bn=
    1an•an+1
    ，n∈N*，Tn为数列{bn}的前n项和．
    （1）求数列{an}的通项公式an和数列{bn}的前n项和Tn；
    （2）若对任意的n∈N*，不等式λTn＜n+8•(-1)n恒成立，求实数λ的取值范围；
    （3）是否存在正整数m，n（1＜m＜n），使得T1，Tm，Tn成等比数列？若存在，求出所有m，n的值；若不存在，请说明理由．

    查看答案和解析>>

    科目： 来源： 题型：

    已知椭圆C：
    x2
    a2
    +
    y2
    b2
    =1(a＞b＞0)    的左右焦点分别为F1（-1，0）、F2（1，0），且经过点P(1，
    3
    2
    )    ，M为椭圆上的动点，以M为圆心，MF2为半径作圆M．
    （1）求椭圆C的方程；
    （2）若圆M与y轴有两个交点，求点M横坐标的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：

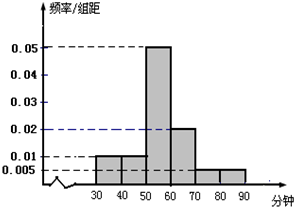    某学校高二年级共有1000名学生，其中男生650人，女生350人，为了调查学生周末的休闲方式，用分层抽样的方法抽查了200名学生．
    （1）完成下面的2×2列联表；
    不喜欢运动 喜欢运动 合计
    女生 50
    男生
    合计 100 200
    （2）在喜欢运动的女生中调查她们的运动时间，发现她们的运动时间介于30分钟到90分钟之间，右图是测量结果的频率分布直方图，若从区间段[40，50）和[60，70）的所有女生中随机抽取两名女生，求她们的运动时间在同一区间段的概率．

    查看答案和解析>>

    科目： 来源： 题型：

    集合P＝｛x」x2－16<0｝,Q＝｛x」x＝2n，nZ｝,则PQ＝

    (A).｛-2,2｝     (B).｛－2，2，－4，4｝    (C).｛2，0，2｝    (D).｛－2，2，0，－4，4｝

    查看答案和解析>>

    科目： 来源： 题型：

    已知锐角△ABC中，内角A，B，C的对边分别为a，b，c，且c=6，sin2C=-
    		3
    cos2C    ，
    （1）求角C的大小；
    （2）若sinA=
    1
    3
    ，求△ABC的面积．

    查看答案和解析>>

    科目： 来源： 题型：

    在极坐标系中，圆ρ=-4cosθ的圆心极坐标为
    （2，π）
    （2，π）
    ．

    查看答案和解析>>

    科目： 来源： 题型：

    已知函数f（x）的定义域为R，对任意s，t∈R都有f（s+t）=f（s）+f（t），且对任意x＞0，都有f（x）＜0，且已知f（3）=-3．
    （1）求证：f（x）是R上的单调递减函数；
    （2）求证：f（x）是奇函数；
    （3）求f（x）在[m，n]（m，n∈Z且m＞0）上的值域．

    查看答案和解析>>

    科目： 来源： 题型：

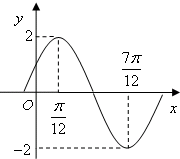    已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
    π2
    ）的部分图象如图所示．
    （1）求f（x）的最小正周期；
    （2）求f（x）的解析式；
    （3）求f（x）的最大值，并求出取最大值时x的值．

    查看答案和解析>>

    科目： 来源： 题型：

    如图，在棱长为1的正方体ABCD-A′B′CD′中，AP=BQ=b（0＜b＜1），截面PQEF∥A′D，截面PQGH∥AD′.

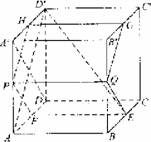
    （Ⅰ）证明：平面PQEF和平面PQGH互相垂直;

    （Ⅱ）证明：截面PQEF和截面PQGH面积之和是定值，并求出这个值;

    （Ⅲ）若，求D′E与平面PQEF所成角的正弦值．

    查看答案和解析>>

    科目： 来源： 题型：

    已知|
    a
    |=4，|
    b
    |=2，且
    a
    与
    b
    的夹角θ为60°，求
    （1）（
    a
    -2
    b
    ）•（
    a
    +3
    b
    ）；
    （2）
    a
    与
    a
    -
    b
    的夹角φ．

    查看答案和解析>>

    同步练习册答案