练习册

  • 练习册
  • 试题
    相关习题
     0  38184  38192  38198  38202  38208  38210  38214  38220  38222  38228  38234  38238  38240  38244  38250  38252  38258  38262  38264  38268  38270  38274  38276  38278  38279  38280  38282  38283  38284  38286  38288  38292  38294  38298  38300  38304  38310  38312  38318  38322  38324  38328  38334  38340  38342  38348  38352  38354  38360  38364  38370  38378  266669 

    科目： 来源： 题型：

    如图，AA1、BB1为圆柱OO1的母线，BC是底面圆O的直径，D、E分别是AA1、CB1的中点．
    （I）证明：DE∥平面ABC；
    （Ⅱ）若BB1=BC=2，求三棱锥A-A1BC的体积的最大值．

    查看答案和解析>>

    科目： 来源： 题型：

    近年空气质量逐步恶化，雾霾天气现象出现增多，大气污染危害加重．大气污染可引起心悸、呼吸困难等心肺疾病．为了解某市心肺疾病是否与性别有关，在某医院随机的对入院50人进行了问卷调查得到了如下的列联表：
    患心肺疾病 不患心肺疾病 合计
    男 5
    女 10
    合计 50
    已知在全部50人中随机抽取1人，抽到患心肺疾病的人的概率为
    3
    5
    ．
    （Ⅰ）请将上面的列联表补充完整；
    （Ⅱ）是否有99.5%的把握认为患心肺疾病与性别有关？说明你的理由；
    （Ⅲ）已知在不患心肺疾病的5位男性中，有3位又患胃病．现在从不患心肺疾病的5位男性中，任意选出3位进行其他方面的排查，求恰好有一位患胃病的概率．
    下面的临界值表供参考：
    P（K2≥k） 0.15 0.10 0.05 0.025 0.010 0.005 0.001
    k 2.072 2.706 3.841 5.024 6.635 7.879 10.828
    （参考公式K2=
    n(ad-bc)2
    (a+b)(c+d)(a+c)(b+d)
    其中n=a+b+c+d）

    查看答案和解析>>

    科目： 来源： 题型：

    已知命题“?x∈R，|x-a|+|x+1|≤2”是假命题，则实数a的取值范围是（　　）

    查看答案和解析>>

    科目： 来源： 题型：

    在△ABC中，已知向量
    AB
    =(cos180，cos720)    ，
    AC
    =(2cos630，2cos270)    ，则cos∠BAC的值为（　　）

    查看答案和解析>>

    科目： 来源： 题型：

    随机抽取某厂的某种产品200件，经质检，其中有一等品126件、二等品50件、三等品20件、次品4件．已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元，而1件次品亏损2万元．设1件产品的利润（单位：万元）为．

    （1）求的分布列；

    （2）求1件产品的平均利润（即的数学期望）；

    （3）经技术革新后，仍有四个等级的产品，但次品率降为1%，一等品率提高为70%．如果此时要求1件产品的平均利润不小于4.73万元，则三等品率最多是多少？

    查看答案和解析>>

    科目： 来源： 题型：

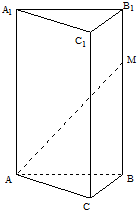    如图，正三棱柱ABC-A1B1C1的底面边长为1，高为h（h＞3），点M在侧棱BB1上移动，并且M到底面ABC的距离为x，且AM与侧面BCC1B1所成的角为α．
    （1）若α在区间[
    π
    6
    ，
    π
    4
    ]    上变化，求x的变化范围； 
    （2）若α为
    π
    6
    ，求AM与BC所成角的余弦值．

    查看答案和解析>>

    科目： 来源： 题型：

    已知斜三棱柱侧棱与底面边长均为2，侧棱与底面所成的角为60°，且侧面ABB1A1与底面垂直．
    （1）求异面直线B1C与C1A所成的角；
    （2）求此斜三棱柱的表面积．

    查看答案和解析>>

    科目： 来源： 题型：

    如图，在棱长为1的正方体ABCD-A1B1C1D1中，E，F分别是A1B1，CD的中点．
    （1）求二面角E-AF-B的大小； 
    （2）求点B到面AEF的距离．

    查看答案和解析>>

    科目： 来源： 题型：

    设，椭圆方程为，抛物线方程为．如图所示，过点作轴的平行线，与抛物线在第一象限的交点为，已知抛物线在点的切线经过椭圆的右焦点．

    （1）求满足条件的椭圆方程和抛物线方程；

    （2）设分别是椭圆长轴的左、右端点，试探究在抛物线上是否存在点P，使得为直角三角形？若存在，请指出共有几个这样的点？并说明理由（不必具体求出这些点的坐标）．

    查看答案和解析>>

    科目： 来源： 题型：

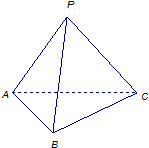    已知边长为
    		2
    的正方形ABCD沿对角线AC折成直二面角，使D到P的位置．
    （1）求直线PA与BC所成的角；
    （2）若M为线段BC上的动点，当BM：BC为何值时，平面PAC与平面PAM所成的锐二面角为45°．

    查看答案和解析>>

    同步练习册答案