已知矩阵A=

2 1 -2 1

，B=

1 -2 0 1

（1）计算AB；
（2）若矩阵B把直线l：x+y+2=0变为直线l'，求直线l'的方程．

（2011•江苏二模）已知各项均为正数的等差数列{a_n}的公差d不等于0，设a₁，a₃，a_k是公比为q的等比数列{b_n}的前三项，
（1）若k=7，a₁=2；
（i）求数列{a_nb_n}的前n项和T_n；
（ii）将数列{a_n}和{b_n}的相同的项去掉，剩下的项依次构成新的数列{c_n}，设其前n项和为S_n，求S2n-n-1-22n-1+3•2n-1(n≥2，n∈N*)的值
（2）若存在m＞k，m∈N^*使得a₁，a₃，a_k，a_m成等比数列，求证k为奇数．

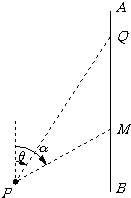（2008•江苏二模）如图，AB是沿太湖南北方向道路，P为太湖中观光岛屿，Q为停车场，PQ=5.2km．某旅游团游览完岛屿后，乘游船回停车场Q，已知游船以13km/h的速度沿方位角θ的方向行驶，sinθ=

5

13

．游船离开观光岛屿3分钟后，因事耽搁没有来得及登上游船的游客甲为了及时赶到停车地点Q与旅游团会合，立即决定租用小船先到达湖滨大道M处，然后乘出租汽车到点Q（设游客甲到达湖滨大道后能立即乘到出租车）．假设游客甲乘小船行驶的方位角是α，出租汽车的速度为66km/h．
（Ⅰ）设sinα=

4

5

，问小船的速度为多少km/h时，游客甲才能和游船同时到达点Q；
（Ⅱ）设小船速度为10km/h，请你替该游客设计小船行驶的方位角α，当角α余弦值的大小是多少时，游客甲能按计划以最短时间到达Q．

如图，用一块形状为半椭圆x2+

y2

4

=1（y≥0）的铁皮截取一个以短轴BC为底的等腰梯形ABCD，记所得等腰梯形的面积为S，则

1

S

的最小值是．

已知a，b，c（a＜b＜c）成等差数列，将其中的两个数交换，得到的三个数依次成等比数列，则

a2+c2

2b2

的值为．

已知函数f（x）=x⁴+ax³+2x²+b，其中a，b∈R．若函数f（x）仅在x=0处有极值，则a的取值范围是．

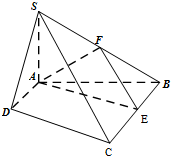如图，四棱锥S-ABCD中，SA⊥平面ABCD，底面ABCD为直角梯形，AD∥BC，∠BAD=90°，且BC=2AD=2，AB=4，SA=3．
（1）求证：平面SBC⊥平面SAB；
（2）若E、F分别为线段BC、SB上的一点（端点除外），满足

BF

BS

=

BE

BC

=λ．（0＜λ＜1）
①求证：对于任意的λ∈（0，1），恒有SC∥平面AEF；
②是否存在λ，使得△AEF为直角三角形，若存在，求出所有符合条件的λ值；若不存在，说明理由．

已知直线l：y=x，圆C₁的圆心为（3，0），且经过（4，1）点．
（1）求圆C₁的方程；
（2）若圆C₂与圆C₁关于直线l对称，点A、B分别为圆C₁、C₂上任意一点，求|AB|的最小值；
（3）已知直线l上一点M在第一象限，两质点P、Q同时从原点出发，点P以每秒1个单位的速度沿x轴正方向运动，点Q以每秒2

2

个单位沿射线OM方向运动，设运动时间为t秒．问：当t为何值时直线PQ与圆C₁相切？