练习册

  • 练习册
  • 试题
    相关习题
     0  41465  41473  41479  41483  41489  41491  41495  41501  41503  41509  41515  41519  41521  41525  41531  41533  41539  41543  41545  41549  41551  41555  41557  41559  41560  41561  41563  41564  41565  41567  41569  41573  41575  41579  41581  41585  41591  41593  41599  41603  41605  41609  41615  41621  41623  41629  41633  41635  41641  41645  41651  41659  266669 

    科目： 来源： 题型：

    现有2门不同的考试要安排在5天之内进行，每天最多进行一门考试，且不能连续两天有考试，那么不同的考试安排方案种数有（　　）

    查看答案和解析>>

    科目： 来源： 题型：

    已知数列{an}的前n项和Sn=log2（n+1），则a4+a5+a6+a7=（　　）

    查看答案和解析>>

    科目： 来源： 题型：

    如图，I是全集，M、P、S是I的3个子集，则阴影部分所表示的集合是

    (A)．（M∩P）∩S          (B)．（M∩P）∪S

    (C)．（M∩P）∩         (D)．（M∩P）∪  

    查看答案和解析>>

    科目： 来源： 题型：

    tan15°-cot15°的值为（　　）

    查看答案和解析>>

    科目： 来源： 题型：

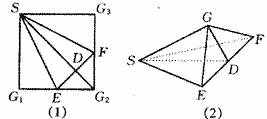
    在边长为1的正方形SG1G2G3中，E，F分别是G1G2及G2G3的中点，D是EF的中点，现在沿SE，SF及EF把这个正方形折成一个由四个三角形围成的“四面体”，使G1，G2，G3三点重合，重合后的点记为G（如下图），那么在四面体S－EFG外接球的半径是

    A．                  B．                   C．                   D．以上都不对

    查看答案和解析>>

    科目： 来源： 题型：

    （选做题）在A，B，C，D四小题中只能选做2题，每小题10分，共计20分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．
    A．选修4-1：几何证明选讲
    如图，⊙O的半径OB垂直于直径AC，M为AO上一点，BM的延长线交⊙O于N，过
    N点的切线交CA的延长线于P．
    （1）求证：PM2=PA•PC；
    （2）若⊙O的半径为2
    		3
    ，OA=
    		3
    OM，求MN的长．
    B．选修4-2：矩阵与变换
    曲线x2+4xy+2y2=1在二阶矩阵M=
    .
    1a
    b1
    .
    的作用下变换为曲线x2-2y2=1，求实数a，b的值；
    C．选修4-4：坐标系与参数方程
    在极坐标系中，圆C的极坐标方程为ρ=
    		2
    cos(θ+
    π
    4
    )    ，以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，直线l的参数方程为
    x=1+
    4
    5
    t 
    y=-1-
    3
    5
    t 
    （t为参数），求直线l被圆C所截得的弦长．
    D．选修4-5：不等式选讲
    设a，b，c均为正实数．
    （1）若a+b+c=1，求a2+b2+c2的最小值；
    （2）求证：
    1
    2a
    +
    1
    2b
    +
    1
    2c
    ≥
    1
    b+c
    +
    1
    c+a
    +
    1
    a+b
    ．

    查看答案和解析>>

    科目： 来源： 题型：

    已知数列{an}满足a1=2，10an+1-9an-1=0，bn=
    9
    10
    (n+2)(an-1)    ．
    （1）求证：数列{an-1}是等比数列；
    （2）当n取何值时，bn取最大值；
    （3）若
    tm
    bm
    ＜
    tm+1
    bm+1
    对任意m∈N*恒成立，求实数t的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：

    设数集,且M,N都是集合的子集,如果把叫做集合的“长度”，那么集合的“长度”的最小值是      

    A．                    B．                   C．                   D．

    查看答案和解析>>

    科目： 来源： 题型：

    已知椭圆C：
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0）的离心率为
    1
    2
    ，且经过点D（1，
    3
    2
    ）．A，B分别是椭圆C的左右顶点，M为椭圆上一点，直线AM，BM分别交椭圆右准线L于P，Q．
    （1）求椭圆C的方程；
    （2）求
    AP
    •
    BQ
    的值
    （3）求|PQ|的最小值．

    查看答案和解析>>

    科目： 来源： 题型：

    如图，四边形ABCD为矩形，AD⊥平面ABEAE=EB=BC=2，F为CE上的点，且BF⊥平面ACE，BD∩AC=G．
    （1）求证：AE⊥平面BCE；
    （2）求证：AE∥平面BFD；
    （3）求四面体BCDF的体积．

    查看答案和解析>>

    同步练习册答案