
科目: 来源: 题型:
查看答案和解析>>
科目: 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
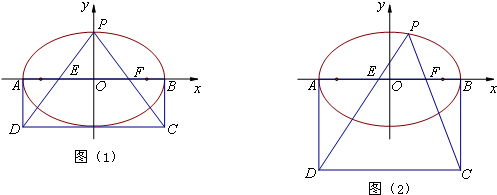
| 6 |
| 5 |
查看答案和解析>>
科目: 来源: 题型:
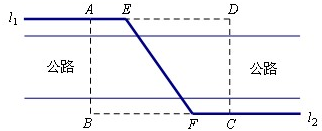
查看答案和解析>>
科目: 来源: 题型:
某银行准备新设一种定期存款业务,经预测,存款量与利率的平方成正比,比例系数为![]() ,贷款的利率为4.8%,又银行吸收的存款能全部放贷出去.
,贷款的利率为4.8%,又银行吸收的存款能全部放贷出去.
(1)若存款的利率为![]() ,试写出存款量
,试写出存款量![]() 及银行应支付给储户的利息
及银行应支付给储户的利息![]() ;
;
(2)存款利率定为多少时,银行可获得最大收益?
查看答案和解析>>
科目: 来源: 题型:
| m |
| n |
| m |
| n |
| CA |
| CB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com