练习册

  • 练习册
  • 试题
    相关习题
     0  44421  44429  44435  44439  44445  44447  44451  44457  44459  44465  44471  44475  44477  44481  44487  44489  44495  44499  44501  44505  44507  44511  44513  44515  44516  44517  44519  44520  44521  44523  44525  44529  44531  44535  44537  44541  44547  44549  44555  44559  44561  44565  44571  44577  44579  44585  44589  44591  44597  44601  44607  44615  266669 

    科目： 来源： 题型：

    已知数列{an}的前n项和为Sn，且a1=1，Sn=nan-2n（n-1），n∈N*．
    （I）求数列{an}的通项公式；
    （II）求数列{
    1an•an+1
    }的前n项和Tn    ．

    查看答案和解析>>

    科目： 来源： 题型：

    若向区域
    y2≤cos2x
    -
    π
    2
    ≤x≤
    π
    2
    内任意投一点P，则点P落在单位圆x2+y2=1内的概率为
    π
    4
    π
    4
    ．

    查看答案和解析>>

    科目： 来源： 题型：

    从4名女生和6名男生中按性别分层抽取5人外出参观，则不同的抽取方法有
    120
    120
    种．

    查看答案和解析>>

    科目： 来源： 题型：

    已知集合A={x|y=
    		2x-x2
    }，B={y|y=3x，x＞0}，定义A*B    为图中阴影部分的集合，则A*B（　　）
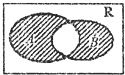
    精英家教网
    A、{x|0＜x＜2}
    B、{x|1＜x≤2}
    C、{x|0≤x≤1或x≥2}
    D、{x|0≤x≤1或x＞2}

    查看答案和解析>>

    科目： 来源： 题型：

    已知z1=3-i，z2=1+i，
    .
    z1
    是z1    的共轭复数，则
    .
    z1
    .
    z2
    =（　　）
    A、1+iB、1-i
    C、2+iD、1+2i

    查看答案和解析>>

    科目： 来源： 题型：

    （2013•淄博一模）已知函数g（x）=（2-a）lnx，h（x）=lnx+ax2（a∈R），令f（x）=g（x）+h′（x）．
    （Ⅰ）当a=0时，求f（x）的极值；
    （Ⅱ）当a＜0时，求f（x）的单调区间；
    （Ⅲ）当-3＜a＜-2时，若存在λ1，λ2∈[1，3]，使得|f（λ1）-f（λ2）|＞（m+ln3）a-2ln3成立，求m的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：

    （2013•淄博一模）已知椭圆c：
    x2
    a2
    +
    y2
    3
    =1（a＞
    		10
    ）的右焦点F在圆D：（x-2）2+y2=1上，直线l：x=my+3（m≠0交椭圆于M、N两点．
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）若
    OM
    ⊥
    ON
    （O为坐标原点），求m的值；
    （Ⅲ）设点N关于x轴的对称点为N1（N1与点M不重合），且直线N1M与x轴交于点P，试问△PMN的面积是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由．

    查看答案和解析>>

    科目： 来源： 题型：

    （2013•淄博一模）设数列[an]的前N项和为Sn，点（an，Sn）在直线y=
    3
    2
    x-1上．
    （Ⅰ）求数列{an}的通项公式；
    （Ⅱ）在an与a n+1之间插入n个数，使这n+2个数组成公差为dn的等差数列，求数列{
    1
    dn
    }的前n项和Tn，并求使
    8
    5
    Tn+
    n
    5×3n-1
    ≤
    40
    27
    成立的正整数n最小值．

    查看答案和解析>>

    科目： 来源： 题型：

    （2013•淄博一模）在一个盒子中，放有大小相同的红、白、黄三个小球，从中任意摸出一球，若是红球记1分，白球记2分，黄球记3分．现从这个盒子中，有放回地先后摸得两球，所得分数分别记为x、y，设o为坐标原点，点p的坐标为（x-2），x-y），记ξ=|
    		OP
    |2．
    （Ⅰ）求随机变量ξ的最大值，并求事件“ξ取得最大值”的概率；
    （Ⅱ）求随机变量ξ的分布列和数学期望．

    查看答案和解析>>

    科目： 来源： 题型：

    对某种赌博游戏调查后，发现其规则如下：摊主在口袋中装入8枚黑色和8枚白色的围棋子，参加者从中随意一次摸出5枚，摸一次交手续费2元，而中彩情况如下：

    摸子情况

    5枚白

    4枚白

    3枚白

    其它

    彩金

    20元

    3元

    纪念品价值1元

    无奖同乐一次

           现在我们试计算如下问题：

       （1）求一次获得20元彩金的概率；（结果用最简分数表示）

       （2）分别求一次获3元和纪念奖的概率；（结果用最简分数表示）

       （3）如果某天有1000次摸奖，估计摊主是赔钱还是挣钱？大概是多少元？

    查看答案和解析>>

    同步练习册答案