
科目: 来源: 题型:
| 1 |
| x |
| 1 |
| x |
| 2n |
 |
| k=1 |
| 1 |
| 2 |
查看答案和解析>>
科目: 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| OP |
| OA |
| OB |
| OP |
| FQ |
查看答案和解析>>
科目: 来源: 题型:
| 1 |
| 2 |
| OAn |
| OBn |
查看答案和解析>>
科目: 来源: 题型:
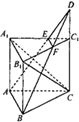 (2013•成都二模)如图,在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,AC=AA1=2AB=2,∠BAC=90°,点D是侧棱CC1 延长线上一点,EF是平面ABD与平面A1B1C1的交线.
(2013•成都二模)如图,在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,AC=AA1=2AB=2,∠BAC=90°,点D是侧棱CC1 延长线上一点,EF是平面ABD与平面A1B1C1的交线.3
| ||
| 14 |
查看答案和解析>>
科目: 来源: 题型:
 (2013•成都二模)如图,某中学甲、乙两班共有25名学生报名参加了一项 测试.这25位学生的考分编成的茎叶图,其中 有一个数据因电脑操作员不小心删掉了(这里暂用x来表示),但他清楚地记得两班学生成绩的中位数相同.
(2013•成都二模)如图,某中学甲、乙两班共有25名学生报名参加了一项 测试.这25位学生的考分编成的茎叶图,其中 有一个数据因电脑操作员不小心删掉了(这里暂用x来表示),但他清楚地记得两班学生成绩的中位数相同.查看答案和解析>>
科目: 来源: 题型:
| 2 |
| π |
| 4 |
查看答案和解析>>
科目: 来源: 题型:
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com