练习册

  • 练习册
  • 试题
    相关习题
     0  44665  44673  44679  44683  44689  44691  44695  44701  44703  44709  44715  44719  44721  44725  44731  44733  44739  44743  44745  44749  44751  44755  44757  44759  44760  44761  44763  44764  44765  44767  44769  44773  44775  44779  44781  44785  44791  44793  44799  44803  44805  44809  44815  44821  44823  44829  44833  44835  44841  44845  44851  44859  266669 

    科目： 来源： 题型：

    方程组
    2x+y=1
    3x-2y=0
    对应的增广矩阵为
     
    ．

    查看答案和解析>>

    科目： 来源： 题型：

    已知平面，定点P之间的距离为8，则在内到P点的距离为10点的轨迹是                  

    A．一个圆            B．两条直线            C．四个点           D．两个点

    查看答案和解析>>

    科目： 来源： 题型：

    2010年11月广州成功举办了第十六届亚运会．在华南理工大学学生会举行的亚运知识有奖问答比赛中，甲、乙、丙同时回答一道有关亚运知识的问题，已知甲回答对这道题目的概率是
    3
    4
    ，甲、丙两人都回答错的概率是
    1
    12
    ，乙、丙两人都回答对的概率是
    1
    4
    ．
    （1）求乙、丙两人各自回答对这道题目的概率．
    （2）求回答对这道题目的人数的随机变量ξ的分布列和期望．

    查看答案和解析>>

    科目： 来源： 题型：

    如图所示，质点P在正方形ABCD的四个顶点上按逆时针方向前进．现在投掷一个质地均匀、每个面上标有一个数字的正方体玩具，它的六个面上分别写有两个1、两个2、两个3一共六个数字．质点P从A点出发，规则如下：当正方体上底面出现的数字是1，质点P前进一步（如由A到B）；当正方体上底面出现的数字是2，质点P前进两步（如由A到C）；当正方体上底面出现的数字是3，质点P前进三步（如由A到D）．在质点P转一圈之前连续投掷，若超过一圈，则投掷终止．
    求：
    （Ⅰ）需要四次投掷，点P恰返回到A点的概率；
    （Ⅱ）点P恰好返回到A点的概率．

    查看答案和解析>>

    科目： 来源： 题型：

    学校要用三辆车从北湖校区把教师接到文庙校区，已知从北湖校区到文庙校区有两条公路，汽车走公路①堵车的概率为
    1
    4
    ，不堵车的概率为
    3
    4
    ；汽车走公路②堵车的概率为p，不堵车的概率为1-p，若甲、乙两辆汽车走公路①，丙汽车由于其他原因走公路②，且三辆车是否堵车相互之间没有影响．
    （I）若三辆车中恰有一辆车被堵的概率为
    7
    16
    ，求走公路②堵车的概率；
    （Ⅱ）在（I）的条件下，求三辆车中被堵车辆的个数为2的概率．

    查看答案和解析>>

    科目： 来源： 题型：

    某种家用电器每台的销售利润与该电器的无故障使用时间有关，每台这种家用电器若无故障使用时间不超过一年，则销售利润为0元，若无故障使用时间超过一年不超过三年，则销售利润为100元；若无故障使用时间超过三年，则销售利润为200元．
    已知每台该种电器的无故障使用时间不超过一年的概率为
    1
    5
    ，无故障使用时间超过一年不超过三年的概率为
    2
    5
    ．
    （I）求销售两台这种家用电器的销售利润总和为400元的概率；
    （II）求销售三台这种家用电器的销售利润总和为300元的概率．

    查看答案和解析>>

    科目： 来源： 题型：

    已知三棱锥P-ABC中，PC⊥底面ABC，∠ABC=90°，AB=BC=2，二面角P-AB-C为450，D、F分别为AC、PC的中点，DE⊥AP于E．
    （Ⅰ）求证：AP⊥平面BDE；
    （Ⅱ）求直线EB与平面PAC所成的角．

    查看答案和解析>>

    科目： 来源： 题型：

    已知椭圆的左、右焦点分别为F1、F2，且|F1F2|=2c，点A在椭圆上，，，则椭圆的离心率=                                               

    A．                          B．              C．              D．

    查看答案和解析>>

    科目： 来源： 题型：

    （2011•新余二模）已知函数f(x)=
    		3
    sinωx+cos(ωx+
    π
    3
    )+cos(ωx-
    π
    3
    )-1    （ω＞0，x∈R），且函数f（x）的最小正周期为π．
    （1）求函数f（x）的解析式并求f（x）的最小值；
    （2）在△ABC中，角A，B，C所对的边分别为a，b，c，若f（B）=1，
    BA
    •
    BC
    =
    9
    2
    ，且a+c=3+
    		3
    ，求边长b．

    查看答案和解析>>

    科目： 来源： 题型：

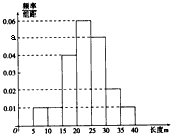    （2011•顺义区二模）某棉纺厂为了解一批棉花的质量，从中随机抽测100根棉花纤维的长度（棉花纤维的长度是棉花质量的重要指标）．所得数据均在区间[5，40]中，其频率分布直方图如图所示，由图中数据可知a=
    0.05
    0.05
    ，在抽测的100根中，棉花纤维的长度在[20，30]内的有
    55
    55
    根．

    查看答案和解析>>

    同步练习册答案