已知m=（x-lnx-y，a），

n

=（

1

x

+lnx+15，1），其中a＞0，且a≠1，当时，y关于x的函数关系式记为y=f（x）；
（1）写出函数f（x）的解析式，并讨论f（x）的单调性；
（2）设函数g（x）=

(-2x3-3ax2-6ax-4a2+6a)   ex，x≤1 e•f(x)，x＞

1（e是自然数的底数）．是否存在正整数a，使g（x）在[-a，a]上为减函数？若存在，求出所有满足条件的正整数a；若不存在，请说明理由．

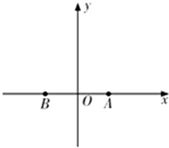为了加快县域经济的发展，某县选择两乡镇作为龙头带动周边乡镇的发展，决定在这两个镇的周边修建环形高速公路，假设一个单位距离为10km，两镇的中心A、B相距8个单位距离，环形高速公路所在的曲线为E，且E上的点到A、B的距离之和为10个单位距离，在曲线E上建一个加油站M与一个收费站N，使M、N、B三点在一条直线上，并且AM+AN=12个单位距离．
（1） 建立如图的直角坐标系，求曲线E的方程及M、N之间的距离有多少个单位距离；
（2）A、B之间有一条笔直公路Z与AB所在直线成45°，且与曲线E交于P，Q两点，该县招商部门引进外资在四边形PAQB区域开发旅游业，试问最大的开发区域是多少？（平方单位距离）

如图所示，四棱锥P-ABCD的底面是梯形，且BA1AD，CD丄AD，CD=2AB，PA 丄底面 ABCD，E 为 PC 的中点，PA=AD=AB=1．
（1）证明：EB∥平面PAD；
（2）求直线BD与平面PDC所成角的大小．

在2008年北京奥运会某项目的选拔比赛中, 、两个代表队进行对抗赛, 每队三名队员, 队队员是队队员是按以往多次比赛的统计, 对阵队员之间胜负概率如下表, 现按表中对阵方式出场进行三场比赛, 每场胜队得1分, 负队得0分, 设A队、B队最后所得总分分别为、, 且.

（Ⅰ）求A队得分为2分的概率；

（Ⅱ）求的分布列;并用统计学的知识说明哪个队实力较强.

为了丰富同学们的课余生活，长郡中学开展了诸多社团活动，现用分层抽样的方法从“国家政治研究社”，“街舞”，“魔术”，“羽毛球”四个社团中抽取若干人组成校社团指导小组，有关数据见下表（单位：人）

社团	相关人数	抽取人数
国家政治研究社	24	a
街舞	18	3
魔术	b	5
羽毛球	12	C

（1） 求abc的值；
（2） 若从“国家政治研究社”与“羽毛球”社团已抽取的人中选2人担任指导小组组长，求这2人分别来自这两个社团的概率．