科目： 来源： 题型：

科目： 来源： 题型：

（2010•聊城一模）如图，在直角梯形ABEF中，将四边形DCEF沿CD折起，使∠FDA=60°，得到一个空间几何体如图所示．
（1）求证：BE∥平面ADF；
（2）求证：AF⊥平面ABCD；
（3）求三棱锥E-BCD的体积．

科目： 来源： 题型：

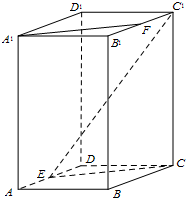（2012•昌平区二模）在正四棱柱ABCD-A₁B₁C₁D₁中，E为AD中点，F为B₁C₁中点．
（Ⅰ）求证：A₁F∥平面ECC₁；
（Ⅱ）在CD上是否存在一点G，使BG⊥平面ECC₁？若存在，请确定点G的位置，并证明你的结论；若不存在，请说明理由．

科目： 来源： 题型：

如图所示的多面体ABCDE中，已知AB∥DE，AB⊥AD，△ACD是正三角形，AD=DE=2AB=2，BC=

5

，F是CD的中点．
（1）求证：AF∥平面BCE；
（2）求直线CE与平面ABED所成角的余弦值；
（3）求多面体ABCDE的体积．

科目： 来源： 题型：

如图所示，正方体ABCD-A₁B₁C₁D₁，E，F分别是AD，AA₁的中点．
（1）求直线EF和直线AB₁所成的角的大小；
（2）求二面角D-A₁C₁-D₁的正切值．

科目： 来源： 题型：

科目： 来源： 题型：

如图所示，已知三棱锥P-ABC的各顶点均在一个半径为R的球面上，球心0在AB上，P0⊥平面ABC，

AB

BC

=

3

，则三棱锥与球的体积之比为

3

：8π

3

：8π

．

科目： 来源： 题型：

一个三棱锥的三视图，如图所示，则该三棱锥的外接球的体积为

9

2

π

9

2

π

．

科目： 来源： 题型：

如图，三棱锥V-ABC的底面为正三角形，侧面VAC与底面垂直且VA=VC，已知其主视图的面积为

2

3

，则其左视图的面积为

3

3

3

3

．

科目： 来源： 题型：

如图是一个几何体的平面展开图，其中ABCD为正方形，E、F分别为PA、PD的中点，在此几何体中，给出下面四个结论：
①直线BE与直线CF异面；
②直线BE与直线AF异面；
③直线EF∥平面PBC；     
④平面BCE⊥平面PAD．
其中正确结论的个数是（　　）

A．1个

B．2个

C．3个

D．4个