练习册

  • 练习册
  • 试题
    相关习题
     0  46127  46135  46141  46145  46151  46153  46157  46163  46165  46171  46177  46181  46183  46187  46193  46195  46201  46205  46207  46211  46213  46217  46219  46221  46222  46223  46225  46226  46227  46229  46231  46235  46237  46241  46243  46247  46253  46255  46261  46265  46267  46271  46277  46283  46285  46291  46295  46297  46303  46307  46313  46321  266669 

    科目： 来源： 题型：

    为了了解学生遵守《中华人民共和国交通安全法》的情况，调查部门在某学校进行了如下的随机调查：向被调查者提出两个问题：（1）你的学号是奇数吗？（2）在过路口的时候你是否闯过红灯？要求被调查者背对调查人员抛掷一枚硬币，如果出现正面，就回答第（1）个问题，否则就回答第（2）个问题。被调查者不必告诉调查人员自己回答的是哪一个问题，只需要回答“是”或“不是”，因为只有被调查者本人知道回答了哪个问题，所以都如实做了回答。结果被调查的600人（学号从1到600）中有180人回答了“是”，由此可以估计在这600人中闯过红灯的人数是

    A．30                                                             B．60

    C．120                                                           D．150

    查看答案和解析>>

    科目： 来源： 题型：

    （2012•洛阳模拟）设f（x）=ln（|x-1|+m|x-2|-3）（m∈R）
    （Ⅰ）当m=1时，求函数f（x）的定义域；
    （Ⅱ）若当1≤x≤
    74
    ，f（x）≥0恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：

    （2012•洛阳模拟）已知函数f（x）=lnx-ax+
    1-a
    x
    -1    （a∈R）．
    （Ⅰ）当a＜
    1
    2
    时，讨论f（x）的单调性；
    （Ⅱ）当a=0时，对于任意的n∈N+，且n≥2，证明：不等式
    1
    f(2)
    +
    1
    f(3)
    +…+
    1
    f(n)
    ＞
    3
    4
    -
    2n+1
    2n(n+1)
    ．

    查看答案和解析>>

    科目： 来源： 题型：

    设函数（为常数），且在上单调递减.

       （1）求实数的取值范围；

       （2）当取得最大值时，关于的方程有3个不同的根，求实数的取值范围。

    查看答案和解析>>

    科目： 来源： 题型：

    （2012•洛阳模拟）如图，四棱锥P-ABCD的底面ABCD为菱形，PA⊥平面ABCD，PA=PB=2，E、F分别为CD、PB的中点，AE=
    		3
    ．
    （Ⅰ）求证：平面AEF⊥平面PAB．
    （Ⅱ）求平面PAB与平面PCD所成的锐二面角的余弦值．

    查看答案和解析>>

    科目： 来源： 题型：

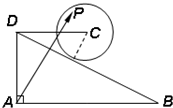    （2012•洛阳模拟）如图，在直角梯形ABCD中，AD⊥AB，AB∥DC，AD=DC=1，AB=2，动点P在以点C为圆心，且与直线BD相切的圆上或圆内移动，设
    AP
    =λ
    AD
    +μ
    AB
    （λ，μ∈R），则λ+μ取值范围是（　　）

    查看答案和解析>>

    科目： 来源： 题型：

    已知函数f（x）=ax4+bx3+cx2+dx+e（a，b，c，d，∈R）是定义在R上的奇函数，且f（x）在x=
    		2
    处取得极小值-
    4
    		2
    3
    ．设f′（x）表示f（x）的导函数，定义数列{an}满足：an=f′（
    		n
    ）+2（n∈N*））．
    （Ⅰ）求数列{an}的通项公式an；
    （Ⅱ）对任意m，n∈N*，若m≤n，证明：1+
    m
    an
    ≤（1+
    1
    an
    ）m＜3；
    （Ⅲ）（理科）试比较（1+
    1
    an
    ）m+1与（1+
    1
    an+1
    ）m+2的大小．

    查看答案和解析>>

    科目： 来源： 题型：

    已知焦点在x轴上椭圆的长轴的端点分别为A，B，O为椭圆的中心，F为右焦点，且
    AF
    •
    BF
    =-1    ，离心率e=
    		2
    2
    ．
    （Ⅰ）求椭圆的标准方程；
    （Ⅱ）记椭圆的上顶点为M，直线l交椭圆于P，Q两点，问：是否存在直线l，使点F恰好为△PQM的垂心？若存在，求出直线l的方程，若不存在，请说明理由．

    查看答案和解析>>

    科目： 来源： 题型：

    （2013•蓟县一模）已知数列{an}中，a1=1，a1+2a2+3a3+…+nan=
    n+12
    an+1(n∈N*)
    （1）求数列{an}的通项an；
    （2）求数列{n2an}的前n项和Tn；
    （3）若存在n∈N*，使得an≥（n+1）λ成立，求实数λ的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：

    某品牌专卖店准备在国庆期间举行促销活动，根据市场调查，该店决定从2种不同型号的洗衣机，2种不同型号的电视机和3种不同型号的空调中（不同种商品的型号不同），选出4种不同型号的商品进行促销，该店对选出的商品采用的促销方案是有奖销售，即在该商品现价的基础上将价格提高150元，同时，若顾客购买任何一种型号的商品，则允许有3次抽奖的机会，若中奖，则每次中奖都获得m（m＞0）元奖金．假设顾客每次抽奖时获奖与否的概率都是
    12
    ，
    （Ⅰ）求选出的4种不同型号商品中，洗衣机、电视机、空调都至少有一种型号的概率；
    （Ⅱ）（文科）若顾客购买两种不同型号的商品，求中奖奖金至少2m元的概率；
         （理科）设顾客在三次抽奖中所获得的奖金总额（单位：元）为随机变量X．请写出X的分布列，并求X的数学期望；
    （Ⅲ）（理科）在（Ⅱ）的条件下，问该店若想采用此促销方案获利，则每次中奖奖金要低于多少元？

    查看答案和解析>>

    同步练习册答案