练习册

  • 练习册
  • 试题
    相关习题
     0  46217  46225  46231  46235  46241  46243  46247  46253  46255  46261  46267  46271  46273  46277  46283  46285  46291  46295  46297  46301  46303  46307  46309  46311  46312  46313  46315  46316  46317  46319  46321  46325  46327  46331  46333  46337  46343  46345  46351  46355  46357  46361  46367  46373  46375  46381  46385  46387  46393  46397  46403  46411  266669 

    科目： 来源： 题型：

    设命题p：非零向量
    a
    ，
    b
    ，|
    a
    |=|
    b
    |    是(
    a
    +
    b
    )⊥(
    a
    -
    b
    )    的充要条件；命题q：“x＞1”是“x＞3”的充要条件，则（　　）

    查看答案和解析>>

    科目： 来源： 题型：

    已知函数f（x）=ln（1+x）-x；
    （I）求证：对?a＞0，f（x）≤ax2；
    （II）证明：ln（n+1）≤
    2
    12
    +
    3
    22
    +
    4
    32
    +…+
    n+1
    n2
    ，（n∈N*）；
    （III）求证：对?t∈R，e2x-2t（ex+x）+x2+2t2-
    1
    2
    ≥0．

    查看答案和解析>>

    科目： 来源： 题型：

    已知P是圆F1：（x+1）2+y2=16上的动点，点F2（1，0），线段PF2的垂直平分线l与半径F1P交于点Q．
    （I）当点P在圆上运动时，求点Q的轨迹C的方程．
    （II）已知点M（1，
    3
    2
    ），A、B在（1）中所求的曲线C上，且
    MA
    +
    MB
    =λ
    OM
    （λ∈R，O是坐标原点），
    （i）求直线AB的斜率；
    （ii）求证：当△MAB的面积取得最大值时，O是△MAB的重心．

    查看答案和解析>>

    科目： 来源： 题型：

    已知数列{an}的前n项和为Sn，且a1=8，Sn=16-kan，n∈N*．
    （I）求k的值及an；
    （II）设f（n）=
    an     (n为奇数)
    log2f(
    n
    2
    )   (n为偶数)
    ，bn=f（2n+1）（n∈N*）
    （i）求bn；      
    （ii）令cn=（bn-3）log2an，求{cn}的前n项和为Tn．

    查看答案和解析>>

    科目： 来源： 题型：

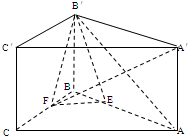    如图，在直三棱柱ABC-A′B′C′中，AB=BC=BB′=a，∠ABC=90°，点E、F分别是棱AB、BC上的动点，且AE=BF．
    （I）求证：A′F⊥AB′．
    （II）当三棱锥B′-BEF的体积取得最大值时，求二面角B-B′F-E的余弦值．

    查看答案和解析>>

    科目： 来源： 题型：

    选做题：考生在下面两小题中，任选一道作答，如果全做则按第1小题评分．
    （1）《几何证明选讲》选做题
    如图，半径分别为a和3a的圆O1与圆O2外切于T，自圆O2上一点P引圆O1的切线，切点为Q，若PQ=2a，则PT=
    2
    		6
    3
    a
    2
    		6
    3
    a
    ．
    （2）《坐标系与参数方程》选做题
    从极点O作射线交直线ρcosθ=3于点M，P为线段OM上的点，且|OM|•|OP|=12，则P点轨迹的极坐标方程为
    p=4cosθ
    p=4cosθ
    ．

    查看答案和解析>>

    科目： 来源： 题型：

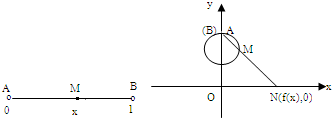    设区间（0，1）内的实数x对应数轴上的点M（如图），将线段AB围成一个圆，使两端A、B恰好重合，再将这个圆放在平面直角坐标系中，使其圆心在y轴上，点A的坐标为（0，1），射线AM与ox轴交于点N（f（x），0）根据这一映射法则可得f（x）与x的函数关系式为
    f（x）=
    cosπx
    sinπx
    ，x∈（0，1）
    f（x）=
    cosπx
    sinπx
    ，x∈（0，1）
    ．

    查看答案和解析>>

    科目： 来源： 题型：

    患感冒与昼夜温差大小相关，居居小区诊所的某医生记录了四月份四个周一的温差情况与因患感冒到诊所看病的人数如下表：
    昼夜温差x（℃） 11 13 12 8
    感冒就诊人数y（人） 25 29 26 16
    用最小二乘法求出y关于x的线性回归方程为
    y=
    18
    7
    x-
    30
    7
    y=
    18
    7
    x-
    30
    7
    ．
    （参考公式：
    b=
    n
    i=1
    (xi-
    .
    x
    )(yi-
    .
    y
    )
    n
    i=1
    (xi-
    .
    x
    )2     
    a=
    .
    y
    -b
    .
    x
    ．）

    查看答案和解析>>

    科目： 来源： 题型：

    已知空间直角坐标系0-xyz中的动点P（x，y，z）满足：x+
    		2
    y+z=1，则|OP|的最小值等于
    1
    2
    1
    2
    ．

    查看答案和解析>>

    科目： 来源： 题型：

    已知二项式(
    		x
    +
    a
    x
    )    6    展开式的常数项为
    ∫
    π
    6
    0
    5cos3tdt    ，则a=
    ±
    1
    3
    ±
    1
    3
    ．

    查看答案和解析>>

    同步练习册答案