科目： 来源： 题型：

科目： 来源： 题型：

（2012•江苏二模）如图，在长方体ABCD-A₁B₁C₁D₁中，AB=4，AD=2，AA₁=2，F是棱BC的中点，点E在棱C₁D₁上，且D₁E=λEC₁（λ为实数）．
（1）当λ=

1

3

时，求直线EF与平面D₁AC所成角的正弦值的大小；
（2）求证：直线EF不可能与直线EA垂直．

科目： 来源： 题型：

（2012•江苏二模）选做题
A．选修4-1：几何证明选讲
如图，自⊙O外一点P作⊙O的切线PC和割线PBA，点C为切点，割线PBA交⊙O于A，B两点，点O在AB上．作CD⊥AB，垂足为点D．
求证：

PC

PA

=

BD

DC

．
B．选修4-2：矩阵与变换
设a，b∈R，若矩阵A=

a 0 -1 b

把直线l：y=2x-4变换为直线l′：y=x-12，求a，b的值．
C．选修4-4：坐标系与参数方程
求椭圆C：

x2

16

+

y2

9

=1上的点P到直线l：3x+4y+18=0的距离的最小值．
D．选修4-5不等式选讲
已知非负实数x，y，z满足x²+y²+z²+x+2y+3z=

13

4

，求x+y+z的最大值．

科目： 来源： 题型：

科目： 来源： 题型：

科目： 来源： 题型：

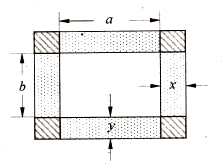（2012•江苏二模）如图，已知矩形油画的长为a，宽为b．在该矩形油画的四边镶金箔，四个角（图中斜线区域）装饰矩形木雕，制成一幅矩形壁画．设壁画的左右两边金箔的宽为x，上下两边金箔的宽为y，壁画的总面积为S．
（1）用x，y，a，b表示S；
（2）若S为定值，为节约金箔用量，应使四个矩形木雕的总面积最大．求四个矩形木雕总面积的最大值及对应的x，y的值．

科目： 来源： 题型：

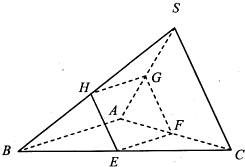（2012•江苏二模）如图，在三棱锥S-ABC，平面EFGHBC，CA，AS，SB交与点E，F，G，H，且SA⊥平面EFGH，SA⊥AB，EF⊥FG．
（1）AB∥平面EFGH；
（2）GH∥EF；
（3）GH⊥平面SAC．

科目： 来源： 题型：

（2012•江苏二模）如图，在四边形ABCD中，已知AB=13，AC=10，AD=5，CD=

65

，

AB

•

AC

=50
（1）求cos∠BAC的值；
（2）求sin∠CAD的值；
（3）求△BAD的面积．

科目： 来源： 题型：

科目： 来源： 题型：