练习册

  • 练习册
  • 试题
    相关习题
     0  46555  46563  46569  46573  46579  46581  46585  46591  46593  46599  46605  46609  46611  46615  46621  46623  46629  46633  46635  46639  46641  46645  46647  46649  46650  46651  46653  46654  46655  46657  46659  46663  46665  46669  46671  46675  46681  46683  46689  46693  46695  46699  46705  46711  46713  46719  46723  46725  46731  46735  46741  46749  266669 

    科目： 来源： 题型：

    （2012•枣庄一模）已知21=2，22=4，23=8，…，则22012个位上的数字为（　　）

    查看答案和解析>>

    科目： 来源： 题型：

    （2012•枣庄一模）已知合集U=R，集合A={y|y=sinx，x∈R}和B=[0，1]，则图中阴影部分表示的集合为（　　）

    查看答案和解析>>

    科目： 来源： 题型：

    设函数f（x）=-x3+ax2+a2x+1（x∈R），其中a∈R．
    （I）当a=1时，求曲线y=f（x）在点（2，f（2））处的切线方程；
    （Ⅱ）当a＞0时，求函数f（x）的极大值和极小值；
    （III）当a=2时，是否存在函数y=f（x）图象上两点以及函数y=f′（x）图象上两点，使得以这四点为顶点的四边形ABCD同时满足如下三个条件：①四边形ABCD是平行四边形：②AB⊥x轴；③|AB|=4．若存在，指出四边形ABCD的个数；若不存在，说明理由．

    查看答案和解析>>

    科目： 来源： 题型：

    如图，在棱长为 的正方体ABCD-A1B1C1D1中， E、F、G分别是CB．CD．CC1的中点．

      

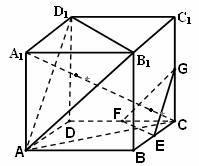
    （1）求直线 A1C与平面ABCD所成角的正弦的值；

       （2）求证：平面A B1D1∥平面EFG；

       （3）求证：平面AA1C⊥面EFG ．

    查看答案和解析>>

    科目： 来源： 题型：

    已知点A（-1，O），B（1，0），动点M的轨迹曲线C满足∠AMB=2θ，|
    AM
    |•|
    BM
    |cos2θ=3    ．
    （I）求曲线C的方程；
    （II）试探究曲线C上是否存在点P，使直线PA与PB的斜率kPA•kPB=1？若存在，请指出共有几个这样的点？并说明理由（不必具体求出这些点的坐标）．

    查看答案和解析>>

    科目： 来源： 题型：

    已知数列{an}的前n项为和Sn，点(n，
    Sn
    n
    )    在直线y=
    1
    2
    x+
    11
    2
    上．数列{bn}满足bn+2-2bn+1+bn=0(n∈N*)，且b3=11，前9项和为153．
    （I）求数列{an}、{bn}的通项公式；
    （II）设f(n)=
    an(n=2l-1，l∈N*)
    bn(n=2l，l∈N*)
    ，问是否存在m∈N*，使得f（m+15）=5f（m）成立？若存在，求出m的值；若不存在，请说明理由．

    查看答案和解析>>

    科目： 来源： 题型：

    如图，正三棱锥O-ABC的三条侧棱OA，OB，OC两条垂直，且长度为2．E，F分别是AB，AC的中点，H是EF的中点，过EF的一个平面与侧棱OA，OB，OC或其延长线分别相交于A1，B1，C1，已知OA1=
    32
    •
    （Ⅰ）证明：B1C1⊥平面OAH；
    （Ⅱ）求三棱锥O-A1B1C1体积．

    查看答案和解析>>

    科目： 来源： 题型：

    对于任意的实数a、b，记max{a，b}=
    a(a≥b)
    b(a＜b)
    ．设F（x）=max{f（x），g（x）}（x∈R），其中g（x）=
    1
    3
    x    ，y=f（x）是奇函数．当x≥0时，y=f（x）的图象与g（x）的图象如图所示．则下列关于函数y=F（x）的说法中，正确的是（　　）

    查看答案和解析>>

    科目： 来源： 题型：

    通过随机询问110名性别不同的行人，对过马路是愿意走斑线还是愿意走人行天桥进行抽样调查，得到如下的列表：
    男 女 总计
    走天桥 40 20 60
    走斑马线 20 30 50
    总计 60 50 110
    由K2=
    n(ad-bc)2
    (a+b)(c+d)(a+c)(b+d
    •
    )
    ，算得K2=
    110×(40×30-20×20)2
    60×50×60×50
    ≈7.8    ．
    附表：
    P（K2≥k） 0.050 0.010 0.001
    k 3.841 6.635 10.828
    参照附表，得到的正确结论是（　　）

    查看答案和解析>>

    科目： 来源： 题型：

    下列命题中，错误的是（　　）

    查看答案和解析>>

    同步练习册答案