练习册

  • 练习册
  • 试题
    相关习题
     0  46716  46724  46730  46734  46740  46742  46746  46752  46754  46760  46766  46770  46772  46776  46782  46784  46790  46794  46796  46800  46802  46806  46808  46810  46811  46812  46814  46815  46816  46818  46820  46824  46826  46830  46832  46836  46842  46844  46850  46854  46856  46860  46866  46872  46874  46880  46884  46886  46892  46896  46902  46910  266669 

    科目： 来源： 题型：

    （2012•黄山模拟）已知椭圆
    x2
    a2
    +
    y2
    b2
    =1    （a＞b＞0）的离心率e=
    		2
    2
    ，A、B分别为椭圆长轴右端点与短轴上端点，坐标原点O到直线AB的距离为
    		6
    3
    ．
    （Ⅰ）求椭圆的方程；
    （Ⅱ）过P（0，2）作斜率为k的直线交椭圆于不同的两点M、N，设
    PM
    =λ
    PN
    ，记f(λ)=λ+
    1
    λ
    +2    ，求证：（6f（λ）-32）k2=-3f（λ）；
    （Ⅲ）求k与λ的范围．

    查看答案和解析>>

    科目： 来源： 题型：

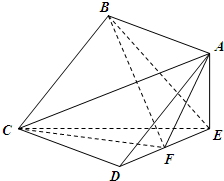    （2012•黄山模拟）如图，在四棱锥E-ABCD中，底面ABCD为正方形，AE⊥平面CDE，已知AE=3，DE=4．
    （Ⅰ）若F为DE的中点，求证：BE∥平面ACF；
    （Ⅱ）求直线BE与平面ABCD所成角的正弦值；
    （Ⅲ）如果四棱锥E-ABCD有外接球，求出四棱锥E-ABCD外接球的半径，没有的话请说明理由．

    查看答案和解析>>

    科目： 来源： 题型：

    （2012•黄山模拟）从一个正方体中截去部分几何体，得到一个以原正方体  的部分顶点为顶点的凸多面体，其三视图如图，则该几何体体积为
    9
    9
    ．

    查看答案和解析>>

    科目： 来源： 题型：

    （2012•黄山模拟）已知函数f（x）的定义域为[-3，+∞），f（6）=1，其导函数的图象如图所示，若正数a，b满足f（2a+b）＜1，则 
    b+2
    a+2
    的取值范围是（　　）

    查看答案和解析>>

    科目： 来源： 题型：

    （2012•黄山模拟）下列说法正确的是（　　）

    查看答案和解析>>

    科目： 来源： 题型：

    设函数f（x）=2ax-bx2+lnx．给出下列条件，条件A：f（x）在x=1 和x=
    1
    2
    处取得极值；条件B：b=a
    （Ⅰ）在A条件下，求出实数a，b的值；
    （Ⅱ） 在A条件下，对于在[
    1
    e
    ，3    ]上的任意x0，不等式f（x0）-c≤0恒成立，求实数c的最小值；
    （Ⅲ） 在B条件下，若f（x）在（0，+∞）上是单调函数，求实数a的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：

    某公司在过去几年内使用某种型号的灯管1000支，该公司对这些灯管的使用寿命（单位：小时）进行了统计，统计结果如下表所示：

    分组

    [500，900)

    [900，1100)

    [1100，1300)

    [1300，1500)

    [1500，1700)

    [1700，1900)

    [1900，)

    频数

    48

    121

    208

    223

    193

    165

    42

    频率

    （I）将各组的频率填入表中；

    （II）根据上述统计结果，计算灯管使用寿命不足1500小时的频率；

    （III）该公司某办公室新安装了这种型号的灯管3支，若将上述频率作为概率，试求至少有2支灯管的使用寿命不足1500小时的概率．

    查看答案和解析>>

    科目： 来源： 题型：

    如图，在直角梯形ABCD中，∠BAD=90°，AD∥BC，AB=2，AD=
    3
    2
    ，BC=
    1
    2
    ，椭圆以A、B为焦点且经过点D．
    （Ⅰ）建立适当的直角坐标系，求椭圆的方程；
    （Ⅱ）以该椭圆的长轴为直径作圆，判断点C与该圆的位置关系．

    查看答案和解析>>

    科目： 来源： 题型：

    （2010•台州二模）以双曲线的焦点为圆心，实轴长为半径的圆与双曲线的渐近线相切，则双曲线的离心率为（　　）

    查看答案和解析>>

    科目： 来源： 题型：

    如图所示，矩形ABCD中，AD⊥平面ABE，AE=EB=BC=2，F为CE上的点，且BF⊥平面ACE
    （1）求证：AE∥平面BFD；
    （2）求二面角D-BE-C的大小；
    （3）求三棱锥C-BGF的体积．

    查看答案和解析>>

    同步练习册答案