
科目: 来源: 题型:
| 2 |
| f′(n-1)-1 |
| 1 |
| an |
| 1 |
| e |
| 1 |
| an |
| 1 |
| an |
查看答案和解析>>
科目: 来源: 题型:
| x |
| 4 |
| 4 | 2 |
| 1 |
| 4 |
查看答案和解析>>
科目: 来源: 题型:
 如图,△VAC中,VC⊥AC,将其绕直线VC旋转得到△VBC,D是AB的中点,AB=
如图,△VAC中,VC⊥AC,将其绕直线VC旋转得到△VBC,D是AB的中点,AB=| 2 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| BE |
| BV |
查看答案和解析>>
科目: 来源: 题型:
查看答案和解析>>
科目: 来源: 题型:
|
| 1 |
| an |
| (y-1)2 |
| 4 |
| a |
| b |
| a |
| b |
查看答案和解析>>
科目: 来源: 题型:
| f(x)•f(y)+1 |
| f(y)-f(x) |
查看答案和解析>>
科目: 来源: 题型:
| x | a |
查看答案和解析>>
科目: 来源: 题型:
已知正方体ABCD―![]() 中,E为棱CC
中,E为棱CC![]() 上的动点,
上的动点,
(1)求证:![]() ⊥
⊥![]() ;
;
(2)当E恰为棱CC![]() 的中点时,求证:平面
的中点时,求证:平面![]() ⊥
⊥![]() ;
;
(3)在棱CC![]() 上是否存在一个点
上是否存在一个点![]() ,可以使二面角
,可以使二面角![]() 的大小为45°,如果存在,试确定点
的大小为45°,如果存在,试确定点![]() 在棱CC
在棱CC![]() 上的位置;如果不存在,请说明理由
上的位置;如果不存在,请说明理由
查看答案和解析>>
科目: 来源: 题型:
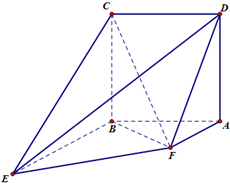 (2012•房山区二模)如图,四边形ABCD为正方形,BE⊥平面ABCD,EB∥FA,FA=AB=
(2012•房山区二模)如图,四边形ABCD为正方形,BE⊥平面ABCD,EB∥FA,FA=AB=| 1 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com