
科目: 来源: 题型:
 (2009•金山区二模)(1)设u、v为实数,证明:u2+v2≥
(2009•金山区二模)(1)设u、v为实数,证明:u2+v2≥| (u+v)2 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目: 来源: 题型:
| Sn | bn |
查看答案和解析>>
科目: 来源: 题型:
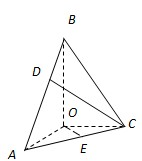 (2009•金山区二模)如图,在三棱锥B-ACO中,BO、AO、CO所在直线两两垂直,且AO=CO,∠BAO=60°,E是AC的中点,三棱锥B-ACO的体积为
(2009•金山区二模)如图,在三棱锥B-ACO中,BO、AO、CO所在直线两两垂直,且AO=CO,∠BAO=60°,E是AC的中点,三棱锥B-ACO的体积为
| ||
| 6 |
| DC |
| OE |
| 1 |
| 4 |
查看答案和解析>>
科目: 来源: 题型:
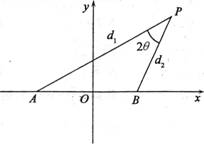 设动点P到点A(-l,0)和B(1,0)的距离分别为d1和d2,∠APB=2θ,且存在常数λ(0<λ<1),使得d1d2 sin2θ=λ.
设动点P到点A(-l,0)和B(1,0)的距离分别为d1和d2,∠APB=2θ,且存在常数λ(0<λ<1),使得d1d2 sin2θ=λ.
(1)证明:动点P的轨迹C为双曲线,并求出C的方程;
(2)过点B作直线交双曲线C的右支于M、N两点,试确定λ的范围,使![]() ?
?![]() =0,其中点O为坐标原点.
=0,其中点O为坐标原点.
查看答案和解析>>
科目: 来源: 题型:
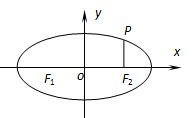 (2009•金山区二模)已知椭圆C:
(2009•金山区二模)已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com