在直角坐标系xOy中.曲线C的参数方程为x=cos2αy=1+2cosα.(α为参数).点M的坐标为,若以该直角坐标系的原点O为极点.x轴的正半轴为极轴建立极坐标系.(Ⅰ)请将点M的直角坐标化为极坐标——青夏教育精英家教网—

相关习题

0 47614 47622 47628 47632 47638 47640 47644 47650 47652 47658 47664 47668 47670 47674 47680 47682 47688 47692 47694 47698 47700 47704 47706 47708 47709 47710 47712 47713 47714 47716 47718 47722 47724 47728 47730 47734 47740 47742 47748 47752 47754 47758 47764 47770 47772 47778 47782 47784 47790 47794 47800 47808 266669

科目： 来源： 题型：

在直角坐标系xOy中，曲线C的参数方程为

x=cos2α

y=1+2cosα.

(α为参数），点M的坐标为（-1，1）；若以该直角坐标系的原点O为极点，x轴的正半轴为极轴建立极坐标系，
（Ⅰ）请将点M的直角坐标化为极坐标（限定ρ≥0，-π＜θ≤π）；
（Ⅱ）若点N是曲线C上的任一点，求线段MN的长度的最大值和最小值．

查看答案和解析>>

科目： 来源： 题型：

已知点A（1，0），B（2，2），C（3，0）．矩阵M表示变换“顺时针旋转45°”，
（Ⅰ）写出矩阵M及其逆阵M^-1；
（Ⅱ）请求出△ABC在矩阵M下所得△A₁B₁C₁的面积．

查看答案和解析>>

科目： 来源： 题型：

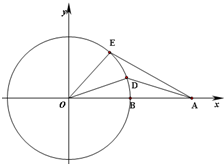如图，已知点A（2，0），B（1，0），点D，E同时从点B出发沿单位圆O逆时针运动，且点E的角速度是点D的角速度的2倍．设∠BOD=θ，0≤θ＜2π
（Ⅰ）当∠BOD=

，求四边形ODAE的面积；
（Ⅱ）将D、E两点间的距离用f（θ）表示，并求f（θ）的单调区间．

查看答案和解析>>

科目： 来源： 题型：

已知函数f(x)（x∈R）满足下列条件：对任意的实数x₁、x₂都有≤[f(x₁)f(x₂)]和|f(x₁) f(x₂)|≤|x₁－x₂|，其中是大于0的常数，设实数a₀，a，b满足f(a₀)=0，b=af(a).

（1）证明≤1，并且不存在b₀≠a₀，使得f(b₀)=0

（2）证明（ba₀）²≤(1²)(aa₀)²

（3）证明[f(b)]²≤(1) [f(a)]²

查看答案和解析>>

科目： 来源： 题型：

（2011•泉州模拟）如图，已知三角形ABC的三边AB=4，AC=5，BC=3，椭圆M以A、B为焦点且经过点C．
（Ⅰ）建立适当直角坐标系，求椭圆M的标准方程；
（Ⅱ）过线段AB的中点的直线l交椭圆M于E，F两点，试求

•

的取值范围．

查看答案和解析>>

科目： 来源： 题型：

（2011•泉州模拟）某研究性学习小组欲从标点符号使用频率的角度研究《A》名著，现抽查了书中的n页，按每页标点符号的个数把样本分成四组：[30，40），[40，50），[50，60），[60，70），相应的频率分布直方图如图所示，已知样本中[30，40）的频数为1．
（Ⅰ）求p、n的值；
（Ⅱ）现从这n页中随机抽取3页，用ξ表示标点符号个数在[60，70）的页数，求ξ的分布列和期望．

查看答案和解析>>

科目： 来源： 题型：

（2011•泉州模拟）“黑白配”游戏，是小朋友最普及的一种游戏，很多时候被当成决定优先权的一种方式．它需要参与游戏的人（三人或三人以上）同时出示手势，以手心（白）、手背（黑）来决定胜负，当其中一个人出示的手势与其它人都不一样时，则这个人胜出，其他情况，则不分胜负．现在甲乙丙三人一起玩“黑白配”游戏．设甲乙丙三人每次都随机出“手心（白）、手背（黑）”中的某一个手势，则一次游戏中甲胜出的概率是

．

查看答案和解析>>

科目： 来源： 题型：

（2011•泉州模拟）已知△ABC中，AC=1，∠ABC=

，D为BC中点，则△ABD的最大面积是

．

查看答案和解析>>

科目： 来源： 题型：

（2011•泉州模拟）圆C的圆心是抛物线x²=4y的焦点，且与抛物线的准线相切，则圆C被y轴截得的弦长是

．

查看答案和解析>>

科目： 来源： 题型：