光线从点A（-3，4）射出，到达直线l：x+y+3=0上的点B后，被直线l反射到y轴上的点C，又被y轴反射，这时的反射光线恰好经过点D（-1，6），求BC的截距式方程．

A、40

B、20（1+ 3 ）

C、30（1+ 3 ）

D、30 3

0

（1）当n∈N⁺时，求证：

1

2

≤

1

n+1

+

1

n+2

+…+

1

2n

＜1；
（2）当n∈N⁺时，求证：1+

1

22

+

1

32

+…+

1

n2

＜2．

A、-6

B、6

C、±4

D、±6

A、 5 -1 2

B、 3 -1 2

C、 3 2

D、 1 2

本题有（1），（2），（3）三个选答题，每题7分，请考生任选2题作答，满分14分．如果多做，则按所做的前两题计分．作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑．
（1）选修4-2：矩阵与变换
如图所示：△OAB在伸缩变换M作用下变为△OA₁B₁．
（i）求矩阵M的特征值及相应的特征向量；
（ii）求逆矩阵M^-1以及（M^-1）²⁰
（2）选修4-4：坐标系与参数方程．
已知曲线C₁的参数方程为

x=2sinθ y=cosθ

（θ为参数），曲线C₂的参数方程为

x=2t y=t+1

（t为参数）
（i）若将曲线C₁与C₂上各点的横坐标都缩短为原来的一半，分别得到曲线C₁和C₂，求出曲线C₁和C₂的普通方程；
（ii）以坐标原点为极点，x轴的非负半轴为极轴建立极坐标系，求过极点且与C₂垂直的直线的极坐标方程．
（3）选修4-5：不等式选讲
已知a，b，c为实数，且a+b+c+2-2m=0，a²+

b 2

4

+

c 2

9

+m-1=0
（i）求证：a²+

b 2

4

+

c 2

9

≥

(a+b+c) 2

14

（ii）求实数m的取值范围．

A、2x-y+1=0

B、2x+y-3=0

C、2x+y-3=0或x-2y-4=0

D、2x-y+1=0或x-2y-4=0

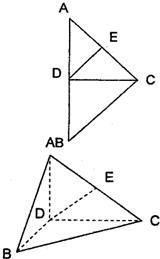如图，在Rt△ABC中，∠ACB=90°，AC=BC=4，D是AB中点，E是AC的中点，现将△ABC沿CD翻折成直二面角A-DC-B．
（1）求异面直线AB与DE所成的角；
（2）若M，N分别为棱AC，BC上的动点，求△DMN周长的平方的最小值；
（3）在三棱锥D-ABC的外接球面上，求A，B两点间的球面距离和外接球体积．

如图，两县城A和B相距20km，O为AB的中点，现要在以O为圆心、20km为半径的圆弧

MN

上选择一点P建造垃圾处理厂，其中MA⊥AB，NB⊥AB．已知垃圾处理厂对城市的影响度与所选地点到城市的距离有关，对城A和城B的总影响度为对城A和城B的影响度之和．统计调查表明：垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比，比例系数为4；对城B的影响度与所选地点到城B的距离的平方成反比，比例系数为9．记垃圾处理厂对城A和城B的总影响度为y，设AP=xkm，∠POA=θ．
（I）写出x关于θ的函数关系，并求该函数的定义域和值域；
（II）当x为多少km时，总影响度最小？