练习册

  • 练习册
  • 试题
    相关习题
     0  48819  48827  48833  48837  48843  48845  48849  48855  48857  48863  48869  48873  48875  48879  48885  48887  48893  48897  48899  48903  48905  48909  48911  48913  48914  48915  48917  48918  48919  48921  48923  48927  48929  48933  48935  48939  48945  48947  48953  48957  48959  48963  48969  48975  48977  48983  48987  48989  48995  48999  49005  49013  266669 

    科目： 来源： 题型：

    某人随机地将编号为1，2，3，4的四个大小相同的小球放入编号为1，2，3，4的四个型号相同的盒子中，每个盒子放一个球，当球的编号与盒子的编号相同时叫做“放法恰当”，否则叫做“放法不恰当”．设放法恰当的情况数为随即变量ξ．
    （1）求ξ的分布列；
    （2）求ξ的期望与方差．

    查看答案和解析>>

    科目： 来源： 题型：

    已知与，若两直线平行，则的值为

    查看答案和解析>>

    科目： 来源： 题型：

    正四棱柱的底面边长为1，侧棱长为
    		3
    ．从正四棱柱的12条棱中任取两条，设η为随机变量，当两条棱相交时，记η=0；当两条棱平行时，η的值为两条棱之间的距离；当两条棱异面时，记η=3．
    （1）求概率p（η=0）；
    （2）求η的分布列，并求其数学期望Eη．

    查看答案和解析>>

    科目： 来源： 题型：

    甲乙两人拿两颗骰子做投掷游戏，规则如下：若掷出的点数之和为3的倍数，原掷骰子的人再继续掷，否则，由对方接着掷．第一次由甲开始掷．
    （1）分别求第二次、第三次由甲掷的概率；
    （2）求前4次抛掷中甲恰好掷两次的概率．

    查看答案和解析>>

    科目： 来源： 题型：

    精英家教网为了调查茂名市某中学高三男学生的身高情况，在该中学高三男学生中随机抽取了40名同学作为样本，测得他们的身高后，画出频率分布直方图如下：
    （1）估计该校高三男生的平均身高；
    （2）从身高在170cm（含170cm）以上的样本中随机抽取2人，记身高在170～175cm之间的人数为X，求X的分布列和数学期望．
    （部分参考数据：167.5×0.125+172.5×0.35+177.5×0.325=139.00）

    查看答案和解析>>

    科目： 来源： 题型：

    有五瓶墨水，其中红色一瓶，蓝色、黑色各两瓶，某同学从中随机任取出两瓶，若取出的两瓶中有一瓶是蓝色，求另一瓶也是蓝色的概率（　　）
    A、
    1
    10
    B、
    1
    7
    C、
    1
    4
    D、
    1
    5

    查看答案和解析>>

    科目： 来源： 题型：

    某超市以每瓶2元的价格购进一种酸奶若干瓶，以每瓶3元的价格售出，如果当天卖不完，余下的酸奶必须倒掉处理．通过市场调查得到100天酸奶日需求量（单位：瓶）的大致数据如下表：
    日销售量n 150 160 170 180 190 200
    天数 15 25 25 12 13 10
    这100天记录的各需求量的频率作为各需求量发生的概率，且每天的需求量互不影响．
    （1）若超市每天购进180瓶酸奶，求连续三天的销售中至少有两天都销售完的概率；
    （2）若超市某一天购进180瓶酸奶，X表示当天的利润（单位：元），求随机变量X的分布列及期望．

    查看答案和解析>>

    科目： 来源： 题型：

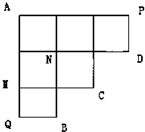    精英家教网如图所示，机器人海宝按照以下程序运行：
    ①从A出发到达点B或C或D，到达点B、C、D之一就停止
    ②每次只向右或向下按路线运行
    ③在每个路口向下的概率
    13

    ④到达P时只向下，到达Q点只向右
    （1）求海宝过点从A经过M到点B的概率，求海宝过点从A经过N到点C的概率；
    （2）记海宝到点B、C、D的事件分别记为X=1，X=2，X=3，求随机变量X的分布列及期望．

    查看答案和解析>>

    科目： 来源： 题型：

    空气质量指数PM2.5（单位：μg/m2）表示每立方米空气中可入肺颗粒的含量，这个值越高，就代表空气污染越严重：
    PM2.5日均浓度 0～35 35～75 75～115 115～150 150～250 ＞250
    空气质量级别 一级 二级 三级 四级 五级 六级
    空气质量类别 优 良 轻度污染 中度污染 重度污染 严重污染
    甲、乙两城市2013年12月份中的15天对空气质量指数PM2.5进行检测，获得PM2.5日均浓度指数数据如茎叶图所示：
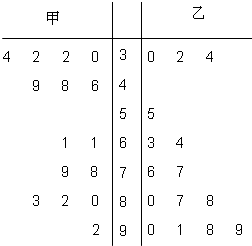
    精英家教网
    （1）在15天内任取1天，估计甲、乙两城市空气质量类别均为优获良的概率；
    （2）在甲城市15个检测数据中任取2个，设X为空气质量类别为优获良的天数，求X的分布列及数学期望（用分数表示）．

    查看答案和解析>>

    科目： 来源： 题型：

    某商场举行抽奖促销活动，抽奖规则是：从装有6个白球，3个黄球，1个红球的箱子中每次随机地摸出一个球，记下颜色后放回，每人最多摸球三次，摸到红球就中止．摸出一个红球可获得奖金50元，摸出一个黄球可获得奖金20元，摸出白球没有奖金．现设X表示甲在这次抽奖活动中获得的奖金总额．
    （1）求P（X＞20）；
    （2）若甲第一次抽得白球，则他在剩下的摸球机会中获得奖金的数学期望是多少？

    查看答案和解析>>

    同步练习册答案