（12分）如图，在梯形ABCD中，平面平面ABCD，四边形ACFE是矩形，AE=a，点M在线段EF上.

（Ⅰ）求证：平面ACFE；

（Ⅱ）当EM为何值时，平面BDF？证明你的结论；

（Ⅲ）求二面角B―EF―D的大小.

（08年衡阳八中文）（13分）

  如图，直角梯形ABCD中，∠，AD∥BC，AB=2，AD=，BC=. 椭圆F以A、B为焦点且过点D.

（1）建立适当的直角坐标系，求椭圆的方程；

（2）若点E满足,是否存在斜率两点，且，若存在，求K的取值范围；若不存在，说明理由。

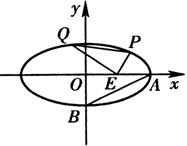
（12分）如图，已知中心在原点O、焦点在x轴上的椭圆C的离心率为，点A、B分别是椭圆C的长轴、短轴的端点，点O到直线AB的距离为

（Ⅰ）求椭圆C的方程；

（Ⅱ）已知点E（3，0），设点P、Q是椭圆C上的两个动点，满足，求的最小值.

（12分）在奥运会射箭决赛中，参赛号码为1~4号的四名射箭运动员参加射箭比赛。

   （Ⅰ）通过抽签将他们安排到1~4号靶位，试求恰有两名运动员所抽靶位号与其参赛号码相同的概率；

   （Ⅱ）记1号、2号射箭运动员射箭的环数为（所有取值为0，1，2，3．．．，10）分别为、.根据教练员提供的资料，其概率分布如下表：

①若1，2号运动员各射箭一次，求两人中至少有一人命中9环的概率；

（08年衡阳八中文）（13分）

已知函数（）.

     （1）若函数的图象在点P（1，）处的切线的倾斜角为,求在上的最小值；

（12分）在△ABC中，A、B、C的对边分别为a、b、c，且 成等差数列.

（Ⅰ）求B的值；

（Ⅱ）求的范围.

某种基金今天的指数是2，以后每一天的指数都比上一天的指数增加0.2%，则100天以后这种基金的指数约是___________（精确到0.001）.