
科目: 来源: 题型:
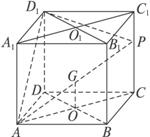
图2-2-8
(1)试确定m,使直线AP与平面BDD1B1所成角的正切值为![]() ;
;
(2)在线段A1C1上是否存在一个定点Q,使得对任意的m,D1Q在平面APD1上的射影垂直于AP,并证明你的结论.
查看答案和解析>>
科目: 来源: 题型:

图2-2-7
(1)求二面角B-AD-F的大小;
(2)求直线BD与EF所成的角.
查看答案和解析>>
科目: 来源: 题型:

图2-2-6
(1)求证:AD⊥BC.
(2)求二面角B-AC-D的大小.
(3)在直线AC上是否存在一点E,使ED与面BCD成30°角?若存在,确定E的位置;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
(1)证明BF∥平面ADE;
(2)若△ACD为正三角形,试判断点A在平面BCDE内的射影G是否在直线EF上,证明你的结论,并求角θ的余弦值.
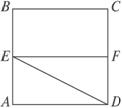

图2-2-4 图2-2-5
查看答案和解析>>
科目: 来源: 题型:
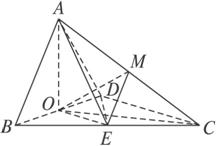
图2-2-4
(1)求证:AO⊥平面BCD;
(2)求异面直线AB与CD所成角的大小;
(3)求点E到平面ACD的距离.
查看答案和解析>>
科目: 来源: 题型:
(1)求证:{an}是等比数列;
(2)若数列{an}的公比q=f(m),数列{bn}满足b1=a1,bn=f(bn-1)(n∈N,n≥2),求证:{![]() }为等差数列.
}为等差数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com