练习册

  • 练习册
  • 试题
    相关习题
     0  53040  53048  53054  53058  53064  53066  53070  53076  53078  53084  53090  53094  53096  53100  53106  53108  53114  53118  53120  53124  53126  53130  53132  53134  53135  53136  53138  53139  53140  53142  53144  53148  53150  53154  53156  53160  53166  53168  53174  53178  53180  53184  53190  53196  53198  53204  53208  53210  53216  53220  53226  53234  266669 

    科目： 来源： 题型：

    如图1-3-10，D是△ABC的AB边上的一点，过点D作DE∥BC交AC于E.已知AD∶DB=2∶3，则S下标△ADE∶S下标BCED为（    ）

    图1-3-10

    A.2∶3            B.4∶9             C.4∶5            D.4∶21

    查看答案和解析>>

    科目： 来源： 题型：

    一块直角三角形木板的一条直角边AB长为1.5米，面积为1.5平方米，要把它加工成一个面积最大的正方形桌面，甲、乙两位同学的加工方法分别如图1-3-9(1)、(2)所示.那么哪位同学的加工方法符合要求？说说你的理由(加工损耗忽略不计，计算结果中的分数可保留).

                 

    (1)                                   (2)

    图1-3-9

    查看答案和解析>>

    科目： 来源： 题型：

    如图1-3-8，小明欲测量一座古塔的高度，他站在该塔的影子上前后移动，直到他本身影子的顶端正好与塔的影子的顶端重叠，此时他距离该塔18 m，已知小明的身高是1.6 m，他的影长是2 m.

    图1-3-8

    (1)图中△ABC与△ADE是否相似?为什么?

    (2)求古塔的高度.

    查看答案和解析>>

    科目： 来源： 题型：

    如图1-3-6，已知在△ABC中，D是BC边上的中点，且AD=AC，DE⊥BC，DE与AB相交于点E，EC与AD相交于点F.

    图1-3-6

    (1)求证:△ABC∽△FCD；

    (2)若S△FCD=5，BC＝10，求DE的长.

    查看答案和解析>>

    科目： 来源： 题型：

    如图1-3-5，已知在△ABC中，AB=AC，∠A=36°，BD是角平分线，试利用三角形相似的关系说明AD2=DC·AC.

    图1-3-5

    查看答案和解析>>

    科目： 来源： 题型：

    如图1-3-4所示，已知D是△ABC中AB边上的一点，DE∥BC且交AC于E，EF∥AB且交BC于F，且S△ADE=1，S△EFC=4，则四边形BFED的面积等于（    ）

    图1-3-4

    A.2              B.4                C.5              D.9

    查看答案和解析>>

    科目： 来源： 题型：

    如图1-3-3，在△ABC中，∠BAC＝90°，D是BC的中点，AE⊥AD交CB延长线于点E，则下列结论正确的是（    ）

    图1-3-3

    A.△AED∽△ACB                  B.△AEB∽△ACD

    C.△BAE∽△ACE                  D.△AEC∽△DAC

    查看答案和解析>>

    科目： 来源： 题型：

    如图1-2-18，△ABC中，D是BC的中点，M是AD上一点，BM、 CM的延长线分别交AC、AB于F、E.求证:EF∥BC.

    图1-2-18

    查看答案和解析>>

    科目： 来源： 题型：

    如图1-2-17（1），已知AB⊥BD，CD⊥BD，垂足分别为B、D，AD和BC相交于点E，EF⊥BD，垂足为F，我们可以证明成立(不要求证明),若将图1-2-17（1）中的垂直改为斜交，如图1-2-17（2），AB∥CD，AD、BC相交于点E，过E作EF∥AB，交BD于点F，则:

    (1)还成立吗？如果成立，请给出证明；如果不成立，请说明理由.(2)请找出S△ABD、S△BED和S△BDC间的关系式，并给出证明.

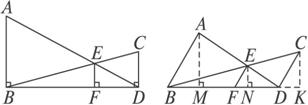
    (1)                                             (2)

                                图1-2-17

    查看答案和解析>>

    科目： 来源： 题型：

    如图1-2-16，在四边形ABCD中，延长AD、BC交于F，延长AB、DC交于E，连结EF，且BD∥EF.求证:AC的延长线必平分EF.

    图1-2-16

    查看答案和解析>>

    同步练习册答案