已知m、n是不重合的直线，α、β是不重合的平面，给出下列四个命题：

①若m⊥α,m⊥β,则α∥β;

②若mα,nβ,m∥n,则α∥β;

③若m∥n,m⊥α,则n⊥α;

④若m⊥α,mβ,则α⊥β.

其中正确命题的个数为(　　)

A.1个　　　　　　　　　

B.2个　　　

C.3个　　　

D.4个

证明：如果两个相交平面分别垂直于两条异面直线中的一条直线，那么这两个平面的交线平行于这两条异面直线的公垂线(交线不是公垂线).

已知：如图,异面直线a和b,a⊥α,b⊥β,α∩β=m,a和b的公垂线为AB，且AB与m不重合.求证：AB∥m.

已知矩形ABCD，过A作SA⊥平面AC，再过A作AE⊥SB交SB于E ，过E作EF⊥SC交SC于F.

（1）求证：AF⊥SC；

（2）若平面AEF交SD于G，求证：AG⊥SD.

四面体ABCD中，AC=BD，E、F分别为AD、BC的中点，且EF=AC,∠BDC=90°

求证：BD⊥平面ACD.

求证：如果一条直线和两个相交平面平行，那么这条直线和它们的交线平行.

已知：α∩β=l,a∥α,a∥β,求证：a∥l.

如图所示，正方体ABCD—A₁B₁C₁D₁中，点N在BD上，点M在B₁C上，且CM=DN.

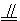
（1）求证：MN∥平面AA₁B₁B；

（2）设正方体ABCD—A₁B₁C₁D₁的棱长为a.问CM为何值时，MN有最小值？并求出最小值.

（1）从平面外一点引平面的一条垂线，这个点和________的距离,叫做这个点到这个平面的距离.?

（2）一条直线和一个平面平行时，这条直线上任意_________到这个平面的_______，叫做这条直线和这个平面的距离.

平面几何中，同垂直于一条直线的两直线________.那么，类比到空间中有：（1）同垂直于一条直线的两条直线平行,这个命题成立吗？______.为什么？_______.（2）同垂直于一个平面的两条直线_________.这个命题是__________（填：真、假）命题.原因是：已知a⊥平面α,b⊥平面α,求证：a∥b.假设b不平行于a,设b∩α=O,b′是经过点O与直线_______平行的直线.∵a_______b′,a⊥α ,?∴b′________α,?即经过同一点O的两条直线________、_______都垂直于平面α，这是不可能的.因此，________.这种证明的方法是________法.?

命题（2）的逆命题是：如果两条平行直线中的一条垂直于一个平面，那么另一条也_________这个平面.用数学符号表示：已知a_____b,a_______平面α,求证：b______α.?

证明：设m是α内的任意一条直线.∵a________α,mα,?

?∴a________m.又∵a_______b,∴________bm.又∵mα,m是_______,∴由线面垂直的__________可知b______α.

如果一条直线和一个平面内的________直线都垂直，那么这条直线和这个平面垂直.该直线叫做__________，该平面叫做________.

下列四个说法是否正确，请给予判断：?

(1)直线l平行于平面α内无数条直线，则l∥α;?

(2)若直线a在平面α外，则a∥α;?

(3)若直线a∥b,直线bα,则a∥α;?

(4)若直线a∥b,bα,那么直线a就平行于平面内的无数条直线.?

这四种说法只有第(4)个是正确的.∵直线l虽与平面α内无数条直线平行，但l有可能_________，∴l不一定平行于α，∴命题(1)是错误的.∵直线a在平面α外，包括两种情况：a∥α 和a与α________,∴a和α不一定平行.∴未必有a∥α,故命题(2)是错误的.直线a∥b,bα,则只能说明a和b_________,但a可能在__________，∴a不一定?平行于α.∴命题(3)也是错误的.对于命题(4)而言，∵a∥b,bα,?∴a______α或a______α.∴a可能与平面α内的无数条直线平行.