
科目: 来源: 题型:
查看答案和解析>>
科目: 来源: 题型:
①正多面体只有5种 ②一个多面体的表面经过连续变形变为球面的多面体,就是简单多面体 ③凸多面体都是简单多面体 ④简单多面体都是凸多面体
A.1 B.2
C.3 D.4
查看答案和解析>>
科目: 来源: 题型:
(1)设二面角B1-EF-B为α,求tanα.?
(2)试问B1B上是否存在一点G,使得D1G⊥平面B1EF?请证明你的结论.?
(3)求三棱锥D1—B1EF的体积.
查看答案和解析>>
科目: 来源: 题型:
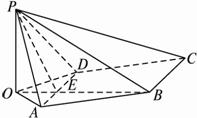
(1)求点P到平面ABCD的距离;
(2)求面APB与面CPB所成二面角的大小.
查看答案和解析>>
科目: 来源: 题型:

(1)求证:AC⊥SB;
(2)若∠AEC为二面角A-SB-C的平面角,求三棱锥E—ABC的体积.
查看答案和解析>>
科目: 来源: 题型:
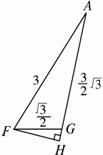
(1)求证:DE⊥平面AGF;
(2)求二面角A-DE-F的大小;
(3)求点F到平面ADE的距离.
查看答案和解析>>
科目: 来源: 题型:
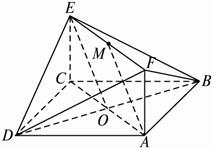
(1)求证:AM∥平面BDE;
(2)求二面角A-DF-B的大小;
(3)试在线段AC上确定一点P,使得PF与BC所成的角是60°.
查看答案和解析>>
科目: 来源: 题型:

(1)试确定D点的位置,并证明你的结论;
(2)求平面AB1D与侧面AB1所成的角及平面AB1D与底面所成的角;
(3)求A1到平面AB1D的距离.
查看答案和解析>>
科目: 来源: 题型:
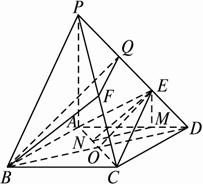
(1)求二面角EACD的?大小?.
(2)在棱PC上是否存在一点F,使BF∥平面AEC?若存在,求出点F;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com