练习册

  • 练习册
  • 试题
    相关习题
     0  56854  56862  56868  56872  56878  56880  56884  56890  56892  56898  56904  56908  56910  56914  56920  56922  56928  56932  56934  56938  56940  56944  56946  56948  56949  56950  56952  56953  56954  56956  56958  56962  56964  56968  56970  56974  56980  56982  56988  56992  56994  56998  57004  57010  57012  57018  57022  57024  57030  57034  57040  57048  266669 

    科目： 来源： 题型：

    在斜三棱柱ABC—A1B1C1的底面ABC中，∠BAC=90°，BC1⊥AC，过C1作C1H⊥底面ABC，垂足为H，则H在…(　　)

    A.直线AC上

    B.直线AB上

    C.直线BC上

    D.△ABC的内部

    查看答案和解析>>

    科目： 来源： 题型：

    一个球与一个正三棱柱的三个侧面和两个底面都相切,已知这个球的体积是,那么这个三棱柱的体积是(　　)

    A.96　 　　B.16　 　　C.24　 　　D.48

    查看答案和解析>>

    科目： 来源： 题型：

    如图，已知矩形ABCD，PA⊥平面ABCD，M、N、R分别是AB、PC、CD的中点.

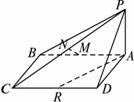
    (1)求证：直线AR∥平面PMC.

    (2)求证：直线MN⊥直线AB.

    (3)若平面PDC与平面ABCD所成的二面角为θ，能否确定θ使直线MN是异面直线AB与PC的公垂线？若能确定，求出θ的值;若不能确定，请说明理由.

    查看答案和解析>>

    科目： 来源： 题型：

    在边长为a的正三角形的三个角处各剪去一个四边形.这个四边形是由两个全等的直角三角形组成的，并且这三个四边形也全等.如：若用剩下的部分折成一个无盖的正三棱柱形容器，如图(2)，则当容器的高为多少时，可使这个容器的容积最大，并求出容积的最大值.

    查看答案和解析>>

    科目： 来源： 题型：

    下图是正方体的平面展开图，在这个正方体中，有以下4个结论：

    ①BM与ED平行；

    ②CN与BE是异面直线；

    ③CN与BM成60°角；

    ④DM与BN垂直.

    正确命题的序号是　　　　　.

    查看答案和解析>>

    科目： 来源： 题型：

    四面体ABCD中,AD=BC=a,　BD=AC=b,　AB=CD=c,以它们为棱,相应两个面为面的二面角依次为α、β、γ.?

           (1)求证:;?

           (2)求四面体ABCD的体积;?

           (3)若a=5,b=4,c=6,求α的正弦值;?

           (4)求AD与平面BCD所成的角〔条件同(3)〕;?

           (5)条件同(3),求四面体的外接球半径.

    查看答案和解析>>

    科目： 来源： 题型：

    已知圆锥外切于半径为1的球，求当圆锥体积最小时它的表面积.

    查看答案和解析>>

    科目： 来源： 题型：

    在四棱锥P—ABCD中，底面ABCD是边长为a的正方形，并且PD=a,　PA=PC=a,

           (1)求证：PD⊥平面ABCD；

           (2)求异面直线PB与AC所成的角；

           (3)求二面角A－PB－D的大小；

           (4)在这个四棱锥中放入一个球，求这个球的最大半径.

    查看答案和解析>>

    科目： 来源： 题型：

    正四棱锥S—ABCD，底面边长为a，侧棱与底面成α角，求它的外接球的表面积.

    查看答案和解析>>

    科目： 来源： 题型：

    A、B、C是半径为1的球面上三点，B、C两点间的距离为，点A与B、C两点间的球面距离均为，且球心为O，求：?

           (1)∠AOB、∠BOC的大小；

           (2)球心到截面ABC的距离.

    查看答案和解析>>

    同步练习册答案