
科目: 来源: 题型:
(1)求动点M的轨迹方程;
(2)若动点M的轨迹在y轴左侧部分与圆心在C(0,a+4)且半径为4的圆相交于两点S、T,求证:C落在以S、T为焦点且过F的椭圆上.
查看答案和解析>>
科目: 来源: 题型:
(1)当k=0时,若g(x)=![]() 的定义域为R,求实数m的取值范围;
的定义域为R,求实数m的取值范围;
(2)给出定理:若函数f(x)在[a,b]上连续,且f(a)·f(b)<0,则函数y=f(x)在区间(a,b)内有零点,即存在x0∈(a,b),使f(x0)=0.运用此定理,试判断当k>1时,函数f(x)在[k,2k]内是否存在零点.
(文)已知数列{an}的前n项和为Sn,a1=2,且nan+1=Sn+n(n+1)(n∈N*).
(1)求an;
(2)设bn=![]() ,求{bn}的最大项.
,求{bn}的最大项.
查看答案和解析>>
科目: 来源: 题型:
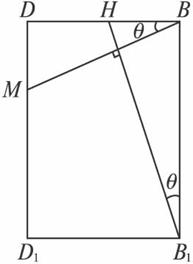
(1)若平面PAB∩平面PCD=l,试判断直线l与平面ABCD的关系,并加以证明;
(2)求平面PAB与平面PCD所成二面角的大小;
(3)当AD为多长时,点D到平面PCE的距离为2?
(文)在正四棱柱ABCD—A1B1C1D1中,BB1=2AB=4,E、F分别是棱AB与BC的中点.
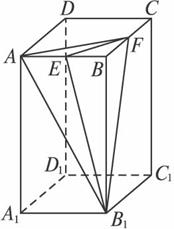
(1)求二面角EFB1B的平面角的正切值.
(2)在棱DD1上能否找到一点M,使BM⊥平面B1EF?若能,试确定M的位置;若不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
(1)甲、乙两人各抛掷一次,谁的点数大谁就胜,求甲获胜的概率;
(2)将这个小正方体抛掷两次,用变量ξ表示向上点数之积,求随机变量ξ的概率分布列及数学期望Eξ.
(文)一个袋中装有大小相同的4个白球和3个黑球.
(1)若采用无放回的方式从袋中任取3个球,求黑球的个数比白球多的概率;
(2)若采用每次抽取都放回的方式逐个抽取3个球,求黑球的个数比白球多的概率.
查看答案和解析>>
科目: 来源: 题型:
(1)求函数f(x)的单调递减区间;
(2)已知△ABC的三边a、b、c对应角为A、B、C,且三角形的面积为S,若![]()
![]() =S,求f(A)的取值范围.
=S,求f(A)的取值范围.
查看答案和解析>>
科目: 来源: 题型:
查看答案和解析>>
科目: 来源: 题型:
![]()
![]()
![]()
![]()
![]()
![]()
… … … … …
查看答案和解析>>
科目: 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com