
科目: 来源: 题型:
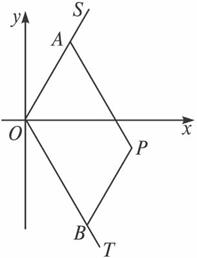
(1)求m·n的值;
(2)求点P的轨迹C的方程,并说明它表示怎样的曲线;
(3)若直线l过点E(2,0)交(2)中曲线C于M、N两点(M、N、E三点互不相同),且![]() ,求l的方程.
,求l的方程.
(文)已知等比数列{an},Sn是其前n项的和,且a1+a3=5,S4=15.
(1)求数列{an}的通项公式;
(2)设bn=![]() +log2an,求数列{bn}的前n项和Tn;
+log2an,求数列{bn}的前n项和Tn;
(3)比较(2)中Tn与![]() n3+2(n=1,2,3,…)的大小,并说明理由.
n3+2(n=1,2,3,…)的大小,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
(1)求a1、a2、a3;
(2)求数列{an}的通项公式;
(3)求证:fn(![]() )<1.
)<1.
(文)设函数f(x)=2ax3-(6a+3)x2+12x(a∈R),
(1)当a=1时,求函数f(x)的极大值和极小值;
(2)若函数f(x)在区间(-∞,1)上是增函数,求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:

(1)求证:EC∥平面APD;
(2)求BP与平面ABCD所成角的正切值;
(3)求二面角PABD的大小.
(文)如图,在三棱锥P—ABC中,PA⊥AB,PA⊥AC,AB⊥AC,PA=AC=2,AB=1,M为PC的中点.
(1)求证:平面PCB⊥平面MAB;

(2)求点A到平面PBC的距离;
(3)求二面角CPBA的正切值.
查看答案和解析>>
科目: 来源: 题型:
(1)如果把10万元投资甲项目,用ξ表示投资收益(收益=回收资金-投资资金),求ξ的概率分布及Eξ;
(2)若把10万元资金投资乙项目的平均收益不低于投资甲项目的平均收益,求α的取值范围.
(文)在某次数学实验中,要求:实验者从装有8个黑球、2个白球的袋中每次随机地摸出一个球,记下颜色后放回.现有甲、乙两名同学,规定甲摸一次,乙摸两次.求
(1)甲摸出白球的概率;
(2)乙恰好摸出一次白球的概率;
(3)甲、乙两人中至少有一个人摸出白球的概率.
查看答案和解析>>
科目: 来源: 题型:

查看答案和解析>>
科目: 来源: 题型:
(1)a1<0,b1>0;
(2)k≥2时,ak与bk满足如下条件:
当ak-1+bk-1≥0时,ak=ak-1,bk=![]() ;
;
当ak-1+bk-1<0时,ak=![]() ,bk=bk-1.
,bk=bk-1.
那么,当a1=-5,b1=5时,{an}的通项公式an=![]() 当b1>b2>…>bn(n≥2)时,且a1、b1表示{bk}的通项bk=_______________(k=2,3,…,n).
当b1>b2>…>bn(n≥2)时,且a1、b1表示{bk}的通项bk=_______________(k=2,3,…,n).
查看答案和解析>>
科目: 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com