
科目: 来源: 题型:
(1)若x1=-1,x2=2,求函数f(x)的解析式;
(2)若|x1|+|x2|=![]() ,求b的最大值;
,求b的最大值;
(3)若x1<x<x2,且x2=a,函数g(x)=f′(x)-a(x-x1),求证:|g(x)|≤![]() a(3a+2)2.
a(3a+2)2.
(文)如图,N为圆x2+(y-2)2=4上的点,OM为直径,连结MN并延长交x轴于点C,过C引直线垂直于x轴,且与弦ON的延长线交于点D.

(1)已知点N(![]() ,1),求点D的坐标;
,1),求点D的坐标;
(2)若点N沿着圆周运动,求点D的轨迹E的方程;
(3)设P(0,a)(a>0),Q是点P关于原点的对称点,直线l过点P交曲线E于A、B两点,点H在射线QB上,且AH⊥PQ,求证:不论l绕点P怎样转动,恒有![]() .
.
查看答案和解析>>
科目: 来源: 题型:
(1)求轨迹E的方程;
(2)若直线l过点F2且与轨迹E交于P、Q两点.
①无论直线l绕点F2怎样转动,在x轴上总存在定点M(m,0),使MP⊥MQ恒成立,求实数m的值.
②过P、Q作直线x=![]() 的垂线PA、QB,垂足分别为A、B,记λ=
的垂线PA、QB,垂足分别为A、B,记λ=![]() ,求λ的取值范围.
,求λ的取值范围.
(文)已知等差数列{an}中,a1=-2,a2=1.
(1)求{an}的通项公式;
(2)调整数列{an}的前三项a1、a2、a3的顺序,使它成为等比数列{bn}的前三项,求{bn}的前n项和.
查看答案和解析>>
科目: 来源: 题型:
(1)请根据以上规律分别写出编号为2和3的同学看到的像;
(2)求编号为n的同学看到的像.
查看答案和解析>>
科目: 来源: 题型:
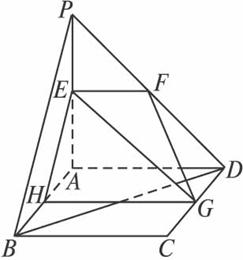
(1)求证:PB∥面EFG;
(2)求异面直线EG与BD所成的角;
(3)在线段CD上是否存在一点Q,使得点A到平面EFQ的距离为0.8.若存在,求出CQ的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
(1)分别写出甲、乙两考生正确完成题数的概率分布列,并计算其数学期望;
(2)试用统计知识分析比较两考生的实验操作能力.
(文)为丰富学生的课余生活,学校决定在高一年级开设系列选修课,并开放了三间多媒体教室,且各门选修课是否使用多媒体教室互不影响.
(1)若周一下午开设的A、B、C三门选修课使用多媒体教室的概率分别为![]() 、
、![]() 、
、![]() ,求这三门选修课中恰有两门课使用多媒体教室的概率;
,求这三门选修课中恰有两门课使用多媒体教室的概率;
(2)若周二下午开设的五门选修课使用多媒体教室的概率均为![]() ,求多媒体教室不够用的概率.
,求多媒体教室不够用的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com