
科目: 来源: 题型:
①若m∥n,m⊥α,则n⊥α;②若m⊥α,m⊥β,则α∥β;③若m⊥α,m∥n,n![]() β,则α⊥β;④若m∥α,α∩β=n,则m∥n.
β,则α⊥β;④若m∥α,α∩β=n,则m∥n.
其中正确命题的个数是
A.0 B.1 C.2 D.3
查看答案和解析>>
科目: 来源: 题型:
A.{1,2,3,4,5} B.{1,4}
C.{1,2,4} D.{3,5}
查看答案和解析>>
科目: 来源: 题型:
①对于任意x∈[0,1],总有f(x)≥3,且f(1)=4;
②若x1≥0,x2≥0,x1+x2≤1,则有f(x1+x2)≥f(x1)+f(x2)-3.
(1)求f(0)的值;
(2)求证:f(x)≤4;
(3)当x∈(![]() ](n=1,2,3,…)时,试证明f(x)<3x+3.
](n=1,2,3,…)时,试证明f(x)<3x+3.
(文)如图,设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A、B两点,且A、B两点坐标为(x1,y1)、(x2,y2),y1>0,y2<0,P是此抛物线的准线上的一点,O是坐标原点.

(1)求证:y1y2=-p2;
(2)直线PA、PF、PB的方向向量为(1,a)、(1,b)、(1,c),求证:实数a、b、c成等差数列;
(3)若![]() =0,∠APF=α,∠BPF=β,∠PFO=θ,求证:θ=|α-β|.
=0,∠APF=α,∠BPF=β,∠PFO=θ,求证:θ=|α-β|.
查看答案和解析>>
科目: 来源: 题型:

(1)试求椭圆的方程;
(2)过F1、F2分别作互相垂直的两直线与椭圆分别交于D、E、M、N四点(如图所示),试求四边形DMEN面积的最大值和最小值.
(文)已知函数f(x)=![]() x3+bx2+cx,b、c∈R,且函数f(x)在区间(-1,1)上单调递增,在区间(1,3)上单调递减.
x3+bx2+cx,b、c∈R,且函数f(x)在区间(-1,1)上单调递增,在区间(1,3)上单调递减.
(1)若b=-2,求c的值;
(2)求证:c≥3;
(3)设函数g(x)=f′(x),当x∈[-1,3]时,g(x)的最小值是-1,求b、c的值.
查看答案和解析>>
科目: 来源: 题型:
(1)求函数f(x)的单调区间;
(2)当0<a<2时,求函数g(x)=f(x)-x2-ax-1在区间[0,3]上的最小值.
(文)已知向量a=(![]() cosx,cosx),b=(0,sinx),c=(sinx,cosx),d=(sinx,sinx).
cosx,cosx),b=(0,sinx),c=(sinx,cosx),d=(sinx,sinx).
(1)当x=![]() 时,求向量a、b的夹角;
时,求向量a、b的夹角;
(2)当x∈[0,![]() ]时,求c·d的最大值;
]时,求c·d的最大值;
(3)设函数f(x)=(a-b)·(c+d),将函数f(x)的图象按向量m平移后得到函数g(x)的图象,且g(x)=2sin2x+1,求|m|的最小值.
查看答案和解析>>
科目: 来源: 题型:
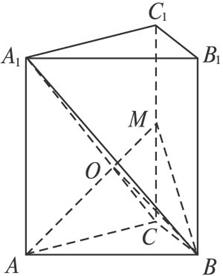
(1)求证:AM⊥平面A1BC;
(2)求二面角B-AM-C的大小;
(3)求点C到平面ABM的距离.
(文)如图,在直三棱柱ABC—A1B1C1中,∠ACB=90°,CB=1,CA=![]() , AA1=
, AA1=![]() ,M为侧棱CC1上一点,AM⊥A1C.
,M为侧棱CC1上一点,AM⊥A1C.
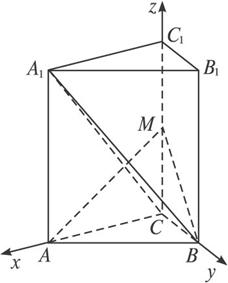
(1)求异面直线A1B与AC所成的角的余弦值;
(2)求证:AM⊥平面A1BC;
(3)求二面角M-AB-C的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com