(1)求点P的轨迹C的方程;

(2)点Q是轨迹C上一点,过点Q的直线l交x轴于点F(-m,0),交y轴于点M,若||=2||,求直线l的斜率.

(文)已知椭圆的中心在坐标原点O,焦点在x轴上,左焦点为F,左准线与x轴的交点为M,.

(1)求椭圆的离心率e;

(2)过左焦点F且斜率为的直线与椭圆交于A、B两点,若=-2,求椭圆的方程.

(1)从盒中任取2个球使用,求恰好取出1个用过的球的概率;

(2)(理)若从盒中任取2个球使用,用完后装回盒中,此时盒中用过的球的个数ξ是一个随机变量,求随机变量ξ的分布列及Eξ.

(文)若从盒中任取2个球使用,用完后装回盒中,求此时盒中恰好有4个是用过的球的概率.

(1)求证:A₁C⊥BE;

(2)求二面角E-BD-C的大小;

(3)求BE与平面A₁D₁C所成角的正弦值.

(文)如图,在长方体ABCD—A₁B₁C₁D₁中,棱AD=DC=3,DD₁=4,E是A₁A的中点.

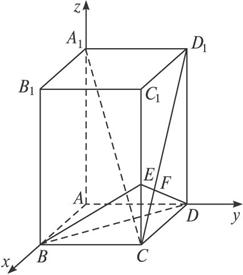
(1)求证:A₁C∥平面BED;

(2)求二面角E-BD-A的大小;

(3)求点E到平面A₁BCD₁的距离.

(1)求b的值;

(2)求a的取值范围.

(文)已知函数f(x)=ax³-x²+bx+2(a、b∈R)在区间(-∞,0)及(4,+∞)上都是增函数,在区间(0,4)上是减函数.

(1)求a、b的值;

(2)求曲线y=f(x)在x=1处的切线方程.

(1)若||=||,求角α的值;

(2)(理)若=-1,求的值.

(文)若()·=2(O是坐标原点),求的值.

①若函数f(x)=a(x³-x)在区间()上为减函数,则a＞0;②函数f(x)=lg(ax+1)的定义域是{x|x＞};③当x＞0且x≠1时,有lnx+≥2;④若M是圆(x-5)²+(y+2)²=34上的任意一点,则点M关于直线y=ax-5a-2的对称点M′也在该圆上.

所有正确命题的序号是___________.

①当x＞0且x≠1时,有lnx+≥2;②函数f(x)=lg(ax+1)的定义域是{x|x＞};

③函数f(x)=e^-xx²在x=2处取得极大值;④圆x²+y²-10x+4y-5=0上任意一点M关于直线ax-y-5a-2=0的对称点M′也在该圆上.

所有正确命题的序号是__________.