
科目: 来源: 题型:
A.若a![]() β,α∥β,则a∥α B.若b
β,α∥β,则a∥α B.若b![]() α,a∥b,则a∥α
α,a∥b,则a∥α
C.若a∥β,α∥β,则a∥α D.若b∥α,a∥b,则a∥α
查看答案和解析>>
科目: 来源: 题型:
(1)求动点P的轨迹方程;
(2)设点P的轨迹为曲线C,过点F作互相垂直的两条直线l1、l2,l1交曲线C于A、B两点,l2交曲线C于M、N两点.求证:![]() +
+![]() 为定值.
为定值.
查看答案和解析>>
科目: 来源: 题型:
(1)若曲线f(x)在点(1,f(1))处的切线与直线2x-y+1=0平行,求a的值;
(2)设g(x)=f′(x)-ax-4,若对一切|a|≤1,都有g(x)<0恒成立,求x的取值范围;
(3)设a=-p2时,若函数f(x)的图象与直线y=2只有一个公共点,求实数p的取值范围.
查看答案和解析>>
科目: 来源: 题型:
(1)求Sn;
(2)设cn=an+8n+3,数列{dn}满足d1=c1,dn+1=![]() (n∈N*),求数列{dn}的通项公式;
(n∈N*),求数列{dn}的通项公式;
(3)设g(x)是定义在正整数集上的函数,对于任意的正整数x1、x2,恒有g(x1x2)=x1g(x2)+x2g(x1)成立,且g(2)=a(a为常数,且a≠0),记bn= ,试判断数列{bn}是否为等差数列,并说明理由.
,试判断数列{bn}是否为等差数列,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
(1)若m=10,求甲袋中红球的个数;
(2)若将甲、乙两袋中的球装在一起后,从中摸出1个球,该球为红球的概率是![]() ,求P2的值;
,求P2的值;
(3)设P2=![]() ,若从甲、乙两袋中各自有放回地摸球,每次摸出1个球,并且从甲袋中摸1次,从乙袋中摸2次,求摸出的3个球中恰有2个红球的概率.
,若从甲、乙两袋中各自有放回地摸球,每次摸出1个球,并且从甲袋中摸1次,从乙袋中摸2次,求摸出的3个球中恰有2个红球的概率.
查看答案和解析>>
科目: 来源: 题型:
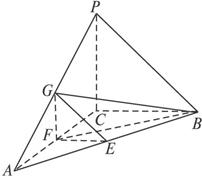
(1)求证:平面GFE∥平面PCB;
(2)求GB与平面ABC所成角的正切值;
(3)求二面角A-PB-C的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com