练习册

  • 练习册
  • 试题
    相关习题
     0  58177  58185  58191  58195  58201  58203  58207  58213  58215  58221  58227  58231  58233  58237  58243  58245  58251  58255  58257  58261  58263  58267  58269  58271  58272  58273  58275  58276  58277  58279  58281  58285  58287  58291  58293  58297  58303  58305  58311  58315  58317  58321  58327  58333  58335  58341  58345  58347  58353  58357  58363  58371  266669 

    科目： 来源： 题型：

    如果等腰三角形的周长是底边长的5倍，那么它的顶角的

    余弦值为（    ）

    A. 5/18            B. 3/4        C. /2      D. 7/8

    查看答案和解析>>

    科目： 来源： 题型：

    已知复数，则（    ）

    A. 2 i             B. －2 i    C. 2       D. －2

    查看答案和解析>>

    科目： 来源： 题型：

    已知函数y=2sin(ωx+)(ω＞0)在区间[0，2π]的图像如下：

    那么ω=（    ）

    A. 1               B. 2               C. 1/2                   D. 1/3

    查看答案和解析>>

    科目： 来源： 题型：

    设p,q为实数,α,β是方程x2-px+q=0的两个实根.数列{xn}满足x1=p,x2=p2-q,xn=pxn-1-qxn-2(n=3,4,…).

    (1)证明α+β=p,αβ=q;

    (2)求数列{xn}的通项公式;

    (3)若p=1,q=,求{xn}的前n项和Sn.

    查看答案和解析>>

    科目： 来源： 题型：

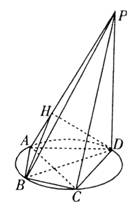
    如图5所示,四棱锥P—ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°.PD垂直底面ABCD,PD=2R.E,F分别是PB,CD上的点,且,过点E作BC的平行线交PC于G.

    图5

    (1)求BD与平面ABP所成角θ的正弦值;

    (2)证明△EFG是直角三角形;

    (3)当=时,求△EFG的面积.

    查看答案和解析>>

    科目： 来源： 题型：

    设k∈R,函数f(x),F(x)=f(x)-kx,x∈R.试讨论函数F(x)的单调性.

    查看答案和解析>>

    科目： 来源： 题型：

    设b＞0,椭圆方程为=1,抛物线方程为x2=8(y-b).如图4所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G.已知抛物线在点G的切线经过椭圆的右焦点F1.

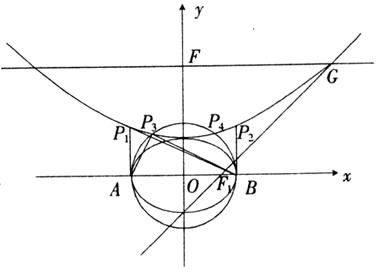
    图4

    (1)求满足条件的椭圆方程和抛物线方程.

    (2)设A、B分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点P,使得△ABP为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).

    查看答案和解析>>

    科目： 来源： 题型：

    随机抽取某厂的某种产品200件,经质检,其中有一等品126件、二等品50件、三等品20件、次品4件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而1件次品亏损2万元.设1件产品的利润(单位:万元)为ξ.

    (1)求ξ的分布列;

    (2)求1件产品的平均利润(即ξ的数学期望);

    (3)经技术革新后,仍有四个等级的产品,但次品率降为1%,一等品率提高为70%.如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?

    查看答案和解析>>

    科目： 来源： 题型：

    已知函数f(x)=Asin(x+φ)(A＞0,0＜φ＜π),x∈R的最大值是1,其图像经过点M(,).

    (1)求f(x)的解析式;

    (2)已知α,β∈(0,),且f(α)=,f(β)=,求f(α-β)的值.

    查看答案和解析>>

    科目： 来源： 题型：

    (几何证明选讲选做题)已知PA是圆O的切线,切点为A,PA=2.AC是圆O的直径,PC与圆O交于点B,PB=1,则圆O的半径R=_____________.

    查看答案和解析>>

    同步练习册答案