练习册

  • 练习册
  • 试题
    相关习题
     0  58670  58678  58684  58688  58694  58696  58700  58706  58708  58714  58720  58724  58726  58730  58736  58738  58744  58748  58750  58754  58756  58760  58762  58764  58765  58766  58768  58769  58770  58772  58774  58778  58780  58784  58786  58790  58796  58798  58804  58808  58810  58814  58820  58826  58828  58834  58838  58840  58846  58850  58856  58864  266669 

    科目： 来源： 题型：

    设等差数列{an}的前n项和是Sn，且a1=10,a2=9，那么下列不等式中成立的是

    A.a10-a11＜0           B.a20+a22＞0           C.S20-S21＜0           D.S40+a41＜0

    查看答案和解析>>

    科目： 来源： 题型：

    已知函数y=2sin(2x+φ)(|φ|＜)的图象经过点(0,1)，则该函数的一条对称轴方程为

    A.x=            B.x=            C.x=            D.x=

    查看答案和解析>>

    科目： 来源： 题型：

    “x2＞4”是“x3＜-8”的

    A.充分不必要条件                         B.必要不充分条件

    C.充要条件                               D.既不充分也不必要条件

    查看答案和解析>>

    科目： 来源： 题型：

    设f(x)=px-2lnx,且f(e)=qe-2(e为自然对数的底数).

    (1)求p与q的关系;

    (2)若f(x)在其定义域内为单调递增函数,求p的取值范围;

    (3)设g(x)=且p＞0,若在［1,e］上至少存在一点x0,使得f(x0)＞g(x0)成立,求实数p的取值范围.

    查看答案和解析>>

    科目： 来源： 题型：

    设数列{an}的前n项和为Sn,已知a1=1,且an+2SnSn-1=0(n≥2).

    (1)求数列{Sn}的通项公式;

    (2)设Sn=,bn=f()+1.记Pn=S1S2+S2S3+…+SnSn+1,Tn=b1b2+b2b3+…+bnbn+1,比较Pn与Tn的大小关系,并给出证明.

    查看答案和解析>>

    科目： 来源： 题型：

    已知F1、F2是双曲线4x2y2=1的左、右焦点,点P是曲线C上任意一点,且||+||=4.

    (1)求曲线C的方程;

    (2)过F2作一直线l交曲线C于A、B两点,若 2=+,求△MF2O面积最大时直线l的方程.

    查看答案和解析>>

    科目： 来源： 题型：

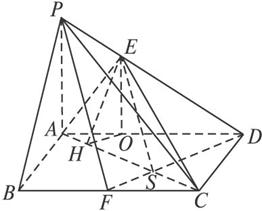
    四棱锥P—ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E点满足PE=.

    (1)求证:PA⊥平面ABCD.

    (2)求二面角E-AC-D的大小;

    (3)在线段BC上是否存在点F使得PF∥面EAC?若存在,确定F的位置;若不存在,请说明理由.

    查看答案和解析>>

    科目： 来源： 题型：

    在中央电视台所举办的北京2008年奥运火炬手的一期选拔节目中,假定每个选手需要进行四轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考核,否则即被淘汰.已知某选手能正确回答第一、二、三、四轮问题的概率分别为,,,,且各轮问题能否回答互不影响.

    (1)求该选手进入第四轮才被淘汰的概率;

    (2)该选手在选拔过程中回答过的问题的总个数记为ξ,求随机变量ξ的分布列与数学期望.

    查看答案和解析>>

    科目： 来源： 题型：

    在△ABC中,三个内角A,B,C所对的边长分别为a,b,c,若向量m=（a,b）与n=(cosA,cosB)共线.

    (1)判断△ABC的形状;

    (2)当y=sin2A+cos(2B)取得最大值时,求角A.

    查看答案和解析>>

    科目： 来源： 题型：

    已知M(-3,0),N(3,0),给出下列曲线:①x-y+5=0;

    ②2x+y-12=0;

    ③x2+y2-12x-8y+51=0;

    ④=1.在所给的曲线上存在点P满足|MP|=10-|NP|的所有曲线方程是___________.

    查看答案和解析>>

    同步练习册答案